题目内容
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+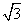 .其中正确的序号是_________________(把你认为正确的都填上).
.其中正确的序号是_________________(把你认为正确的都填上).

①②④ 解析:∵四边形ABCD是正方形,∴AB=AD,又△AEF是等边三角形,∴AE=AF,又∠B=∠D=90°,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=DC,∴BC-BE=CD-DF,∴CE=CF,∴①正确;∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=75°,∴②正确;如下图,连接AC,交EF于点G,∴AC⊥EF,且AC平分EF.∵∠CAF≠∠DAF,∴DF≠FG,∴BE+DF≠EF,∴③错误;∵EF=2,∴CE=CF=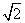 ,设正方形边长为x,在Rt△ADF中,由勾股定理得x2+(x-
,设正方形边长为x,在Rt△ADF中,由勾股定理得x2+(x-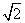 )2=4,解得x=
)2=4,解得x= ,∴x2=(
,∴x2=( )2=2+
)2=2+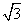 ,即S正方形ABCD=2+
,即S正方形ABCD=2+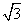 ,∴④正确.
,∴④正确.


练习册系列答案
相关题目
如图10,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为( )
的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为( )
|
| A. | y=x | B. | y= -2x-1 | C. | y=2x-1 | D. | y=-2x+1 |

 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支. ,则
,则 的值为…………………………………………………【 】
的值为…………………………………………………【 】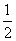 B.﹣
B.﹣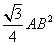 .其中正确的结论有…………………………………【 】
.其中正确的结论有…………………………………【 】 
 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是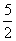 B.x≥
B.x≥ C.x≥
C.x≥