题目内容
20．若$\frac{m}{n}$=$\frac{3}{2}$，则$\frac{m-n}{m}$=$\frac{1}{3}$．分析 根据题意得出$\frac{n}{m}$的值，代入代数式进行计算即可．
解答 解：∵$\frac{m}{n}$=$\frac{3}{2}$，
∴$\frac{n}{m}$=$\frac{2}{3}$，
∴原式=1-$\frac{n}{m}$=1-$\frac{2}{3}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 本题考查的是比例的性质，根据题意得出$\frac{n}{m}$的值是解答此题的关键．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
13．关于抛物线y=ax2和y=-ax2（a≠0），给出下列说法：
①两条抛物线都关于x轴对称；
②两条抛物线都关于原点对称；
③两条抛物线各自关于y轴对称；
④两条抛物线有公共的顶点．
其中正确的说法有（ ）
①两条抛物线都关于x轴对称；
②两条抛物线都关于原点对称；
③两条抛物线各自关于y轴对称；
④两条抛物线有公共的顶点．
其中正确的说法有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．在数轴上距离原点2个单位长度的点所表示的数是（ ）
| A． | ±2 | B． | -2 | C． | 2 | D． | 4 |
8．
如图，在△ABC中，∠ACB=90°，将△ABC绕着点A逆时针旋转得到△ADE，点C落在边AD上，连接BD．若∠DAE=α，则用含α的式子表示∠CBD的大小是（ ）
如图，在△ABC中，∠ACB=90°，将△ABC绕着点A逆时针旋转得到△ADE，点C落在边AD上，连接BD．若∠DAE=α，则用含α的式子表示∠CBD的大小是（ ）| A． | α | B． | 90°-α | C． | $\frac{α}{2}$ | D． | 90$°-\frac{α}{2}$ |
15．
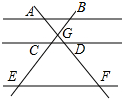如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，那么$\frac{BC}{CE}$的值等于（ ）
如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，那么$\frac{BC}{CE}$的值等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
5．下列二次根式中与$\sqrt{3}$是同类二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{\frac{3}{2}}$ | C． | $\sqrt{\frac{2}{3}}$ | D． | $\sqrt{18}$ |
9．
如图，四边形ABCD内接于圆O，若∠BOD=138°，则它的一个外角∠DCE的度数为（ ）
如图，四边形ABCD内接于圆O，若∠BOD=138°，则它的一个外角∠DCE的度数为（ ）| A． | 138° | B． | 69° | C． | 52° | D． | 42° |
8．如图图形是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |