题目内容
10．把抛物线y=ax2+bx+c的图象先向右平移3个单位长度，再向下平移2个单位长度，所得抛物线是y=2x2-8x-1，则a+b+c的值为（ ）| A． | -1 | B． | 1 | C． | 2 | D． | 3 |
分析 此题可以逆推：将函数y=2x2-8x-1=2（x-2）2-9的图象，先向左平移3个单位长度，再向上平移2个单位长度得到抛物线y=ax2+bx+c．
解答 解：函数y=2x2-8x-1=2（x-2）2-9的图象，先向左平移3个单位长度，再向上平移2个单位长度得到：y=2（x-2+3）2-9+2=2（x+1）2-7，
所以ax2+bx+c=2x2+4x-5，
所以a=2，b=4，c=-5，
所以a+b+c=2+4-5=1．
故选：B．
点评 本题主要考查了函数图象的平移，要求熟练掌握解析式平移的规律：左加右减，上加下减．并用规律求函数解析式．
练习册系列答案
名校课堂系列答案
相关题目
20．如图，四个图形都是由6个大小相同的正方形组成，其中是正方体展开图的是（ ）
| A． | ①②④ | B． | ①②③ | C． | ②④ | D． | ②③④ |
1．把二次函数y=x2的图象向上平移1个单位长度，所得图象相应的函数表达式为（ ）
| A． | y=x2+1 | B． | y=（x+1）2 | C． | y=x2-1 | D． | y=（x-1）2 |
18．已知（4+$\sqrt{7}$）•a=b，若b是整数，则a的值可能是（ ）
| A． | $\sqrt{7}$ | B． | 4+$\sqrt{7}$ | C． | 8-2$\sqrt{7}$ | D． | 2-$\sqrt{7}$ |
5．将点P（-4，-5）先关于y轴对称得P1，将P1关于x轴对称得P2，则P2的坐标为（ ）
| A． | （4，5） | B． | （-4，5） | C． | （4，-5） | D． | （-4，-5） |
15．已知点P的坐标为（-5，6）与点Q关于x轴对称，则点Q的坐标为（ ）
| A． | （-5，-6） | B． | （-5，6 ） | C． | （5，6） | D． | （5，-6） |
19．下列命题中，真命题有（ ）
①同旁内角互补；
②三角形的一个外角等于它的两个内角之和；
③一个三角形的最大角不会小于60°，最小角不会大于60°；
④若函数y=（m+1）x${\;}^{{m}^{2}-3}$是正比例函数，且图象在第二、四象限，则m=-2．
①同旁内角互补；
②三角形的一个外角等于它的两个内角之和；
③一个三角形的最大角不会小于60°，最小角不会大于60°；
④若函数y=（m+1）x${\;}^{{m}^{2}-3}$是正比例函数，且图象在第二、四象限，则m=-2．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．
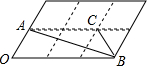如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点，已知菱形的一个角（∠O）为60°，A，B，C都在格点上，则tan∠ABC的值是（ ）
如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点，已知菱形的一个角（∠O）为60°，A，B，C都在格点上，则tan∠ABC的值是（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{2}$ |