题目内容
甲、乙两队开展足球对抗赛,规定每队胜一场得3分,平一场得1分,负一场得0分.甲队与乙队一共举行了10场比赛,甲队保持不败记录,一共得了22分,则甲队胜了 场.
考点:一元一次方程的应用
专题:
分析:设甲队胜了x场,则平了(10-x)场,根据胜一场得3分,平一场得1分,负一场得0分,比赛10场,得分22分,列出不等式,求出x的最小整数解.
解答:解:设甲队胜了x场,则平了(10-x)场,根据题意列方程得
3x+(10-x)=22,
3x+10-x=22,
2x=12,
x=6.
答:甲队胜了6场.
3x+(10-x)=22,
3x+10-x=22,
2x=12,
x=6.
答:甲队胜了6场.
点评:本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出等量关系,列出方程求解.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,则R的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、5 |
 如图,在正方形网格中,将△ABC顺时针旋转后得到△A′B′C′,则下列4个点中能作为旋转中心的是( )
如图,在正方形网格中,将△ABC顺时针旋转后得到△A′B′C′,则下列4个点中能作为旋转中心的是( )| A、点P | B、点Q | C、点R | D、点S |
能清楚的看出每个项目的具体数量的统计图是( )
| A、扇形统计图 |
| B、折线统计图 |
| C、条形统计图 |
| D、以上三种均可 |
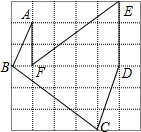 如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示
如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示 如图,∠B=90°,AB=16cm,BC=12cm,AD=21cm,CD=29cm,求图(甲)凸四边形ABCD的面积?把图(甲)改成图(乙)凹四边形ABCD,求图(乙)凹四边形ABCD面积?
如图,∠B=90°,AB=16cm,BC=12cm,AD=21cm,CD=29cm,求图(甲)凸四边形ABCD的面积?把图(甲)改成图(乙)凹四边形ABCD,求图(乙)凹四边形ABCD面积?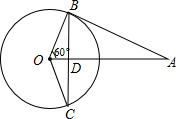 如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.