题目内容
10. (1)解不等式$\left\{\begin{array}{l}{2x+1>-3}\\{\frac{x+3}{5}≤\frac{2x-5}{3}+1}\end{array}\right.$并把不等式组的解集在数轴上表示.
(1)解不等式$\left\{\begin{array}{l}{2x+1>-3}\\{\frac{x+3}{5}≤\frac{2x-5}{3}+1}\end{array}\right.$并把不等式组的解集在数轴上表示.(2)解方程$\frac{x}{{x}^{2}-4}+\frac{2}{x+2}=\frac{1}{x-2}$.
分析 (1)分别求出不等式组中两不等式的解集确定出不等式组的解集,表示在数轴上即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{2x+1>-3①}\\{\frac{x+3}{5}≤\frac{2x-5}{3}+1②}\end{array}\right.$,
由①得:x>-2,
由②得:x≥$\frac{19}{7}$,
∴不等式组的解集为x≥$\frac{19}{7}$,
在数轴上表示为: ;
;
(2)去分母得:x+2(x-2)=x+2,
解得:x=3,
经检验x=3是分式方程的解.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
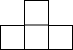
20. 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )
 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
1.下列各数中,最小的数为( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
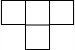
15. 下面几何体的主视图是( )
下面几何体的主视图是( )
 下面几何体的主视图是( )
下面几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.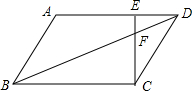 如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
 如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
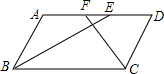 已知:如图,平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则EF=1.
已知:如图,平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则EF=1.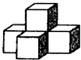 如图是一个由5个相同的正方体组成的立体图形,它的俯视图是( )
如图是一个由5个相同的正方体组成的立体图形,它的俯视图是( )