题目内容
5.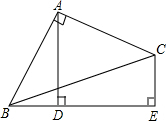 如图,在四边形ABEC中,AB=AC,∠BAC=∠E=90°,AD⊥BE于D.
如图,在四边形ABEC中,AB=AC,∠BAC=∠E=90°,AD⊥BE于D.(1)若BD=3,求AD-CE的值;
(2)若S四ABEC=16,在(1)中,求AB的长.
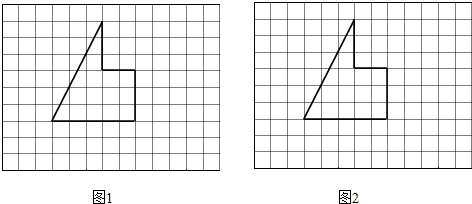
分析 (1)如图1,过C作CF⊥AD于F,则四边形FDEC是矩形,得到DF=CE,通过△ABD≌△ACF,得到AF=BD=3,于是得到结果AD-CE=AD-DF=3;
(2)如图2,过A作AG⊥EC交EC的延长线于G,则四边形ADEG是矩形,同理可证得△ABD≌△ACG,得到AG=AD,S四边形ADEG=S四ABEC=16,推出四边形ADEG是正方形得到AD=4,由勾股定理得到结果AB=$\sqrt{{AD}^{2}{+BD}^{2}}$=5.
解答 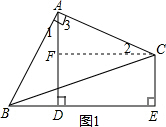 解:(1)如图1,过C作CF⊥AD于F,
解:(1)如图1,过C作CF⊥AD于F,
则四边形FDEC是矩形,
∴DF=CE,
∵∠BAC=90°,
∴∠1+∠3=∠3+∠2=90°,
∴∠1=∠2,
在△ABD与△ACF中,
$\left\{\begin{array}{l}{∠ADB=∠AFC=90°}\\{∠1=∠2}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACF,
∴AF=BD=3,
∴AD-CE=AD-DF=3;
(2)如图2,过A作AG⊥EC交EC的延长线于G,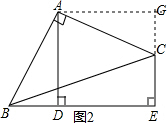
则四边形ADEG是矩形,
同理可证得△ABD≌△ACG,
∴AG=AD,S四边形ADEG=S四ABEC=16,
∴四边形ADEG是正方形,
∴AD=4,
∴AB=$\sqrt{{AD}^{2}{+BD}^{2}}$=5.
点评 本题考查了全等三角形的判定与性质,矩形的性质,正方形的性质,勾股定理,作辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
16.下列各点中在抛物线y=x2-4x-4上的点是( )
| A. | (4,4) | B. | (3,-1) | C. | (-2,-8) | D. | (-$\frac{1}{2}$,-$\frac{7}{4}$) |
13.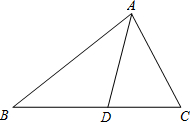 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )| A. | 25° | B. | 35° | C. | 37.5° | D. | 45° |
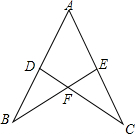 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.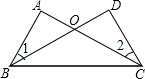 如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.
如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.