Question

15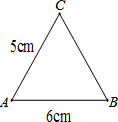．如图，等腰三角形腰长为5cm，底边长为6cm，求三角形的面积．

Answer 1

分析 作CD⊥AB于D，则∠ADC=90°，AD=$\frac{1}{2}$AB=3cm，由勾股定理求出CD，△ABC的面积=$\frac{1}{2}$AB•CD，即可得出结果．

解答 解：作CD⊥AB于D，如图所示：
则∠ADC=90°，AD=$\frac{1}{2}$AB=3cm，
∴CD=$\sqrt{A{C}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4（cm），
∴△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×6×4=12（cm²）．

点评 本题考查了等腰三角形的性质、勾股定理；熟练掌握等腰三角形的性质，并能进行推理计算是解决问题的关键．