题目内容
5.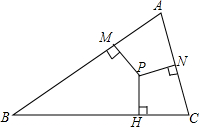 如图,P为△ABC三条角平分线的交点,PH、PN、PM分别垂直于BC、AC、AB,垂足分别为H、N、M.已知△ABC的周长为15cm,PH=3cm,则△ABC的面积为22.5cm2.
如图,P为△ABC三条角平分线的交点,PH、PN、PM分别垂直于BC、AC、AB,垂足分别为H、N、M.已知△ABC的周长为15cm,PH=3cm,则△ABC的面积为22.5cm2.
分析 连接PM、PN、PH,根据角平分线的性质得到PM=PN=PH=3cm,根据三角形的面积公式计算即可.
解答 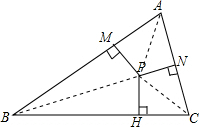 解:连接PM、PN、PH,
解:连接PM、PN、PH,
∵P为△ABC三条角平分线的交点,PH、PN、PM分别垂直于BC、AC、AB,
∴PM=PN=PH=3cm,
∴△ABC的面积=△APB的面积+△BPC的面积+△APC的面积
=$\frac{1}{2}$×AB×PM+$\frac{1}{2}$×BC×PH+$\frac{1}{2}$×AC×PN
=$\frac{1}{2}$(AB+BC+AC)×3
=22.5.
故答案为:22.5.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
16.下列一元二次方程中,没有实根的是( )
| A. | x2+2x-3=0 | B. | x2+x+$\frac{1}{4}$=0 | C. | x2+$\sqrt{2}$x+1=0 | D. | -x2+3=0 |
 如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论:
如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论: 如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.
如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.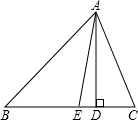 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.