题目内容
6.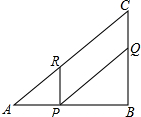 如图,在等腰直角三角形AC中,AB=BC=8cm,一动点P从点A出发,沿AB向点B移动,过点P作PR∥BC,PQ∥AC并分别交AC、BC于点R、Q.
如图,在等腰直角三角形AC中,AB=BC=8cm,一动点P从点A出发,沿AB向点B移动,过点P作PR∥BC,PQ∥AC并分别交AC、BC于点R、Q.(1)四边形PQCR的面积能否为7cm2?如果能,求出点P与点A的距离;如果不能,请说明理由;
(2)四边形PQCR的面积能为16cm2吗?能为20cm2吗?如果能,求出点P与点A的距离;如果不能,请说明理由.
分析 (1)设动点P从A点出发移动x厘米时,?PQCR的面积等于7cm2,根据等腰三角形的性质和平行四边形的面积公式可列方程求解;
(2)利用(1)中的方法建立方程,进一步解方程,根据方程根的情况判定即可.
解答 解:(1)设动点P从A点出发移动x厘米时,?PQCR的面积等于7cm2,依题意有
$\frac{1}{2}$×82-$\frac{1}{2}$x2-$\frac{1}{2}$(8-x)2=7,
解得:x1=1,x2=7.
答:当动点P从A点出发移动1厘米或7厘米时,?PQCR的面积等于7cm2.
(2)由题意得
$\frac{1}{2}$×82-$\frac{1}{2}$x2-$\frac{1}{2}$(8-x)2=16
解得:x1=x2=4,
$\frac{1}{2}$×82-$\frac{1}{2}$x2-$\frac{1}{2}$(8-x)2=20,
此方程无解.
所以当动点P从A点出发移动4厘米时,?PQCR的面积等于16cm2.不存在点P与点A的距离?PQCR的面积等于20cm2.
点评 此题主要考查了一元二次方程的应用,利用三角形和平行四边形的面积得出等量关系是解决问题的关键.

练习册系列答案
相关题目
18.一次函数y=(m+2)x+3m-5不经过第二象限,则m的取值范围是( )
| A. | m≤$\frac{5}{3}$ | B. | m$≥\frac{5}{3}$ | C. | -2<m$≤\frac{5}{3}$ | D. | m≥$\frac{5}{3}$且m≠2 |