题目内容
3.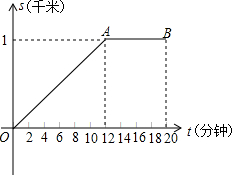 小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.
小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.(1)请解释图中线段AB的实际意义;
(2)试求出小明从家到学校一共走过的路程;
(3)在所给的图中画出s2(千米)与t(分钟)之间函数关系的图象(给相关的点标上字母,指出对应的坐标),并指出图象的形状.
分析 (1)AB段离家距离没发生变化说明在以家为圆心做曲线运动;
(2)由图象可知,当x=12时,y=1,即小明12分钟步行的路程为1千米,所以小明步行的速度为:1÷12=$\frac{1}{12}$(千米/分钟),根据线段AB的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟,求得小明8分钟走的路程为:$\frac{1}{12}×8=\frac{2}{3}$(千米),所以小明从家到学校一共走过的路程为:1+$\frac{2}{3}$=$\frac{5}{3}$(千米).
(3)妈妈的速度正好是小明的2倍,所以妈妈走弧线路用(20-12)÷2=4分钟.
解答 解:(1)图中线段AB的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟;
(2)由图象可知,当x=12时,y=1,即小明12分钟步行的路程为1千米,
∴小明步行的速度为:1÷12=$\frac{1}{12}$(千米/分钟),
∵线段AB的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟,
∴小明8分钟走的路程为:$\frac{1}{12}×8=\frac{2}{3}$(千米),
∴小明从家到学校一共走过的路程为:1+$\frac{2}{3}$=$\frac{5}{3}$(千米).
(3)∵由图象可知,小明花20分钟到达学校,
∴小明的妈妈花20-10=10分钟到达学校,
∴小明妈妈的速度是小明的2倍,
即:小明花12分钟走1千米,则妈妈花6分钟走1千米,
∴D(16,1),
∵小明花20-12=8分钟走圆弧形道路,则妈妈花4分钟走圆弧形道路,
∴B(20,1).
∴妈妈的图象经过(10,0)(16,1)(20,1),
如图中折线段CD-DB就是所作图象.
点评 本题通过考查一次函数的应用来考查从图象上获取信息的能力.特别的作一次函数图象,关键在于确定点,点确定好了,连接就可以得到函数图象.

| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
| A. | (-$\frac{1}{2}$,-$\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{3}$)或(-$\frac{1}{2}$,$\frac{1}{3}$) | D. | (-$\frac{1}{3}$,-$\frac{1}{2}$) |
| 城市 | 北京 | 合肥 | 南京 | 哈尔滨 | 成都 | 南昌 |
| 污染指数 | 354 | 163 | 163 | 45 | 227 | 163 |
| A. | 163和163 | B. | 105和163 | C. | 105和164 | D. | 163和164 |
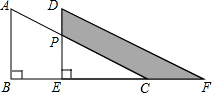 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2.
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2. 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法: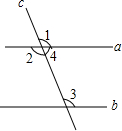 如图所示,已知直线a、b被直线c所截,以下结论:
如图所示,已知直线a、b被直线c所截,以下结论: