Question

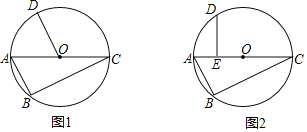
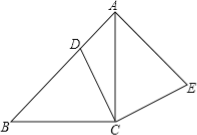
【题目】已知四边形ABCD内接于⊙O，∠DAB＝90°．

（Ⅰ）如图1，连接BD，若⊙O的半径为6，弧AD=弧AB，求AB的长；

（Ⅱ）如图2，连接AC，若AD＝5，AB＝3，对角线AC平分∠DAB，求AC的长．

Answer 1

【答案】（Ⅰ）6；（Ⅱ）4

【解析】

（Ⅰ）如图1，先利用圆周角定理得到BD为直径，即BD＝12，再证明△ABD为等腰直角三角形，然后根据等腰直角三角形求出AB；

（Ⅱ）如图2，连接BD，作BH⊥AC于H，先利用圆周角定理得到BD为直径，利用勾股定理计算出BD＝，再证明△CDB为等腰直角三角形得到BC＝BD＝，接着在Rt△ABH中计算出AH＝BH＝，然后在Rt△BCH中计算出CH＝，从而得到AC的长．

解：（Ⅰ）如图1，

∵∠DAB＝90°，

∴BD为直径，即BD＝12，

∵，

∴AD＝AB，

∴△ABD为等腰直角三角形，

∴AB＝BD＝6；

（Ⅱ）如图2，连接BD，作BH⊥AC于H，

∵∠DAB＝90°，

∴BD为直径，BD＝＝，

∴∠BCD＝90°，

∵AC平分∠DAB，

∴∠BAC＝∠BAC＝45°，

∴∠CBD＝∠BDC＝45°，

∴△CDB为等腰直角三角形，

∴BC＝BD＝×＝，

在Rt△ABH中，AH＝BH＝AB＝，

在Rt△BCH中，CH＝＝，

∴AC＝AH+CH＝＝4．