Question

【题目】如图，在△ABC中，AD是角平分线，点E在AB上，且DE∥CA．

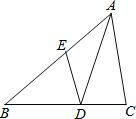
（1）△BDE与△BCA相似吗？为什么？

（2）已知AB＝8，AC＝6，求DE的长．

Answer 1

【答案】（1）△BDE∽△BCA．理由见解析；（2）.

【解析】

（1）根据DE∥AC，得到∠BDE＝∠C，又∠DBE＝∠CBA，故可得△BDE∽△BCA；

（2）先得出ED＝EA，设DE＝x，则AE＝x，BE＝AB﹣AE＝8﹣x，∴，即，解得DE=x＝.

（1）△BDE∽△BCA．理由如下：

∵DE∥AC，

∴∠BDE＝∠C，

而∠DBE＝∠CBA，

∴△BDE∽△BCA；

（2）∵AD是角平分线，

∴∠DAE＝∠DAC，

∵DE∥AC，

∴∠DAC＝∠EDA，

∴∠EDA＝∠DAE，

∴ED＝EA，

设DE＝x，则AE＝x，BE＝AB﹣AE＝8﹣x，

∵△BDE∽△BCA，

∴，即，解得x＝，

即DE的长为．