题目内容
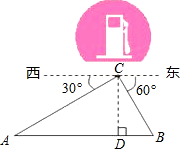
如图是某区“平改坡”工程中一种坡屋顶的设计图．已知原平屋顶的宽度AB为8米，两条相等的斜面钢条AC、BC夹角为110°，过点C作CD⊥AB于D．
（1）求坡屋顶高度CD的长度；
（2）求斜面钢条AC的长度．（长度精确到0.1米）
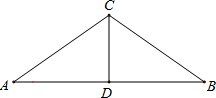
（1）求坡屋顶高度CD的长度；
（2）求斜面钢条AC的长度．（长度精确到0.1米）
（1）∵宽度AB为8米，CD⊥AB于D．
∴AD=
AB=4米，
∵AC、BC夹角为110°，
∴∠ACD=55°，
∵
=tan∠ACD
∴CD=AD÷tan55°=4÷1.43≈2.8米；
（2）在直角三角形ADC中，
∵
=sin∠ACD，
∴AC=
=4÷0.82≈4.9米．
∴AD=
| 1 |
| 2 |
∵AC、BC夹角为110°，
∴∠ACD=55°，
∵
| AD |
| CD |
∴CD=AD÷tan55°=4÷1.43≈2.8米；
（2）在直角三角形ADC中，
∵
| AD |
| AC |
∴AC=
| AD |
| sin55° |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
