题目内容
笔直的公路AB一侧有加油站C，已知从西面入口点A到C的距离60米，西、东两个入口A、B与加油站C之间的方位角如图所示，求加油站C到公路的距离CD及两个入口间的距离AB．
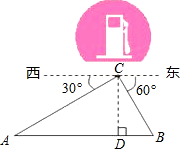
过C作CD⊥AB于D，∵EF∥AB，
∴∠CAD=∠ACE=30°，∠ACF=∠CBD=60°，AC=60米，
∴CD=AC•sin∠ACE=60×
=30米，
由勾股定理得，AD=
=30
米；
在Rt△BCD中，∵∠CBD=60°，
∴BD=30tan30°=10
米，∴AB=AD+BD=40
米．
答：加油站C到公路的距离CD为30米，AB的距离为40
米．
∴∠CAD=∠ACE=30°，∠ACF=∠CBD=60°，AC=60米，
∴CD=AC•sin∠ACE=60×
| 1 |
| 2 |
由勾股定理得，AD=
| 602-302 |
| 3 |
在Rt△BCD中，∵∠CBD=60°，
∴BD=30tan30°=10
| 3 |
| 3 |
答：加油站C到公路的距离CD为30米，AB的距离为40
| 3 |
练习册系列答案
相关题目
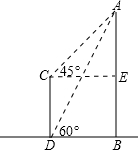高和楼高（精确到0.1m）．（参考数据：
