题目内容
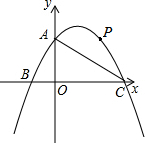 如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,AB=
如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,AB=| 5 |
| 5 |
(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式和对称轴;
(3)设点P是抛物线在第一象限部分上的点,△PAC的面积为S,求使S最大时点P的坐标.
考点:二次函数综合题
专题:
分析:(1)根据勾股定理可求BC,由同角的余角相等得到一对角相等,再由一对公共角相等,得到三角形AOB与三角形CAB相似,由相似得比例,求出OB的长,即可确定出B坐标,进一步得到A、C两点的坐标;
(2)由B与C坐标设出抛物线的交点式,将A坐标代入求出a的值,确定出抛物线解析式,求出对称轴即可;
(3)连接AP,CP,过P作PQ垂直于x轴,设点P(m,n),将x=m代入抛物线解析式表示出P的纵坐标,即为PQ的长,三角形APC面积=梯形APQO面积+三角形PQC面积-三角形AOC面积,列出S关于m的二次函数解析式,利用二次函数的性质求出S最大时m的值,即可确定出此时P的坐标.
(2)由B与C坐标设出抛物线的交点式,将A坐标代入求出a的值,确定出抛物线解析式,求出对称轴即可;
(3)连接AP,CP,过P作PQ垂直于x轴,设点P(m,n),将x=m代入抛物线解析式表示出P的纵坐标,即为PQ的长,三角形APC面积=梯形APQO面积+三角形PQC面积-三角形AOC面积,列出S关于m的二次函数解析式,利用二次函数的性质求出S最大时m的值,即可确定出此时P的坐标.
解答:解:(1)在Rt△ABC中,AB=
,AC=2
,
则BC=
=5,
∵∠AOB=∠BAC=90°,
∴∠ABO+∠BAO=90°,∠ABO+∠ACB=90°,
∴∠BAO=∠ACB,
又∵∠B=∠B,
∴△AOB∽△CAB,
∴
=
,即
=
,解得OB=1,
∴OC=5-1=4,
在Rt△AOB中,AB=
,OB=1,
则OA=
=2,
∴A(0,2),B(-1,0),C(4,0);
(2)设抛物线解析式为y=a(x+1)(x-4),
将A(0,2)代入得:2=-4a,即a=-
,
则过A、B、C三点的抛物线的解析式为y=-
(x+1)(x-4)=-
x2+
x+2,对称轴为直线x=
;
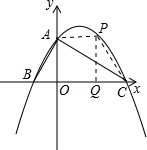 (3)连接AP,CP,过P作PQ⊥x轴,交x轴于点Q,
(3)连接AP,CP,过P作PQ⊥x轴,交x轴于点Q,
设点P(m,n),将x=m代入抛物线解析式得:n=-
m2+
m+2,
∵OA=2,OC=4,OQ=m,PQ=-
m2+
m+4,QC=4-m,
∴S=S△APC=S梯形APQO+S△PQC-S△AOC
=
×m×(2-
m2+
m+4)+
×(4-m)×(-
m2+
m+4)-
×2×4
=-m2+4m+4
=-(m-2)2+8,
∵S关于m的二次函数解析式中二次项系数为-1<0,即抛物线开口向下,
∴当m=2时,S最大值为8,此时P(2,3).
| 5 |
| 5 |
则BC=
| AB2+AC2 |
∵∠AOB=∠BAC=90°,
∴∠ABO+∠BAO=90°,∠ABO+∠ACB=90°,
∴∠BAO=∠ACB,
又∵∠B=∠B,
∴△AOB∽△CAB,
∴
| AB |
| CB |
| OB |
| AB |
| ||
| 5 |
| OB | ||
|
∴OC=5-1=4,
在Rt△AOB中,AB=
| 5 |
则OA=
| AB2-OB2 |
∴A(0,2),B(-1,0),C(4,0);
(2)设抛物线解析式为y=a(x+1)(x-4),
将A(0,2)代入得:2=-4a,即a=-
| 1 |
| 2 |
则过A、B、C三点的抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
 (3)连接AP,CP,过P作PQ⊥x轴,交x轴于点Q,
(3)连接AP,CP,过P作PQ⊥x轴,交x轴于点Q,设点P(m,n),将x=m代入抛物线解析式得:n=-
| 1 |
| 2 |
| 3 |
| 2 |
∵OA=2,OC=4,OQ=m,PQ=-
| 1 |
| 2 |
| 3 |
| 2 |
∴S=S△APC=S梯形APQO+S△PQC-S△AOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=-m2+4m+4
=-(m-2)2+8,
∵S关于m的二次函数解析式中二次项系数为-1<0,即抛物线开口向下,
∴当m=2时,S最大值为8,此时P(2,3).
点评:考查了二次函数综合题,涉及的知识有:相似三角形的判定与性质,待定系数法确定抛物线解析式,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
相关题目
 观察下面由组成的图案和算式,解答问题
观察下面由组成的图案和算式,解答问题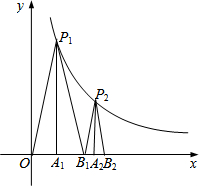 如图,在反比例函数
如图,在反比例函数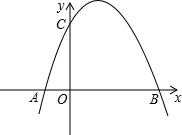 如图,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,3)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,3)两点,与x轴交于另一点B. 如图所示,已知△ABC是等边三角形,D、E分别是AC、BC上的点,∠BDE=60°.
如图所示,已知△ABC是等边三角形,D、E分别是AC、BC上的点,∠BDE=60°.