题目内容
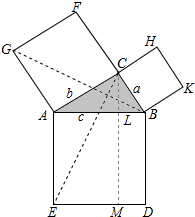 关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法是欧几里得证法.如图所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.
关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法是欧几里得证法.如图所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.(1)叙述勾股定理并结合图形写出已知、求证;
(2)根据图中所添加的辅助线证明勾股定理.
考点:勾股定理的证明
专题:计算题
分析:(1)根据题意写出已知与求证即可;
(2)过C引CM∥BD,交AB于L,连接BG,CE,由∠GAC=∠BAE=90°,得到夹角相等,利用SAS得到三角形ABG与三角形ACE全等,得到三角形ACE与三角形AGB全等,利用三角形面积公式及正方形面积公式变形得到矩形AEML面积等于b2,同理得到矩形BDML面积等于a2,再利用正方形ABDE面积等于矩形AEML面积加上矩形BDML面积,即可得证.
(2)过C引CM∥BD,交AB于L,连接BG,CE,由∠GAC=∠BAE=90°,得到夹角相等,利用SAS得到三角形ABG与三角形ACE全等,得到三角形ACE与三角形AGB全等,利用三角形面积公式及正方形面积公式变形得到矩形AEML面积等于b2,同理得到矩形BDML面积等于a2,再利用正方形ABDE面积等于矩形AEML面积加上矩形BDML面积,即可得证.
解答:解:(1)已知:如图所示,在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2,
求证:a2+b2=c2,
(2)证明:过C引CM∥BD,交AB于L,连接BG,CE,
∵∠GAC=∠BAE=90°,
∴∠GAC+∠CAB=∠BAE+∠CAB,即∠GAB=∠CAE,
在△ACE和△AGB中,
,
∴△ACE≌△AGB(SAS),
∵S△ACE=
AE•EM=
S矩形AEML,S△ABG=
AG•GF=
S正方形ACFG=
b2,
∴S矩形AEML=b2,
同理S矩形BLMD=a2,
∴S正方形ABDE=S矩形AEML+S矩形BLMD=a2+b2,
则a2+b2=c2.
求证:a2+b2=c2,
(2)证明:过C引CM∥BD,交AB于L,连接BG,CE,
∵∠GAC=∠BAE=90°,
∴∠GAC+∠CAB=∠BAE+∠CAB,即∠GAB=∠CAE,
在△ACE和△AGB中,
|
∴△ACE≌△AGB(SAS),
∵S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S矩形AEML=b2,
同理S矩形BLMD=a2,
∴S正方形ABDE=S矩形AEML+S矩形BLMD=a2+b2,
则a2+b2=c2.
点评:此题考查了勾股定理的证明,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,已知AB=CD,AB∥CD,直线EF交AD于点E,交BC于点F,求证:∠1=∠2.
如图,已知AB=CD,AB∥CD,直线EF交AD于点E,交BC于点F,求证:∠1=∠2.