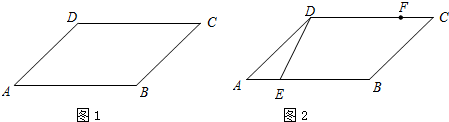题目内容
⊙O的半径为10,AB为⊙O的弦,OC⊥AB于C,AD⊥OB于D,当AB的大小发生变化时,猜一猜OC2+CD2的值是否发生变化,若不变,求出这个定值;若发生变化,求其变化的范围.
考点:垂径定理,直角三角形斜边上的中线,勾股定理
专题:
分析:根据题意画出图形,先根据垂径定理得出C为AB的中点,再根据直角三角形的性质得出CD=
AB,字啊根据勾股定理即可得出结论.
| 1 |
| 2 |
解答: 解:不变.
解:不变.
理由:∵OC⊥AB,
∴C为AB的中点,
∵AD⊥OB,
∴CD=
AB,
∵OC2=OB2-BC2=100-
AB2,
∴OC2+CD2=100-
AB2+
AB2=100.
 解:不变.
解:不变.理由:∵OC⊥AB,
∴C为AB的中点,
∵AD⊥OB,
∴CD=
| 1 |
| 2 |
∵OC2=OB2-BC2=100-
| 1 |
| 4 |
∴OC2+CD2=100-
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查的是垂径定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF.
如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF. 如图,△ABC和△A′B′C′中,AB=A′B′,BC=B′C′,点D、D′分别是BC、B′C′的中点,且AD=A′D′,求证:∠B=∠B′.
如图,△ABC和△A′B′C′中,AB=A′B′,BC=B′C′,点D、D′分别是BC、B′C′的中点,且AD=A′D′,求证:∠B=∠B′.