题目内容
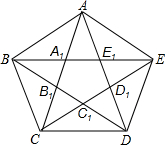 如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )
如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )| A、3 | B、4 | C、5 | D、6 |
考点:全等三角形的判定,正多边形和圆
专题:探究型
分析:先根据正多边形的特点及全等三角形的判定定理找出不同类别的全等三角形即可.
解答:解:∵五边形ABCDE是正五边形,
∴AB=AE=BC=DE,∠ABC=∠AED,
∴△ABC≌△AED,
同理可得,△ABC≌△AED≌△BCD;
故△ABC,△AED,△BCD是同一个全等类;
∵△ABC≌△AED,
∴∠BAC=∠EAD,
∵AB=AE,
∴∠ABE=∠AEB,
∵AB=AE,
∴△ABA1≌△AEE1,
∴△ABA1与△AEE1属于一个全等类;
同理可得△ABE1≌△AEA1,△AA1E1≌△CB1C1,△ACD≌△CEA它们分别属于一个全等类.
∵△BC1E≌△ABE,
∴△ABC≌△AED,与△BC1E≌△ABE属于同一个全等类.
故图中不同全等类的个数为5个.
故选C.
∴AB=AE=BC=DE,∠ABC=∠AED,
∴△ABC≌△AED,
同理可得,△ABC≌△AED≌△BCD;
故△ABC,△AED,△BCD是同一个全等类;
∵△ABC≌△AED,
∴∠BAC=∠EAD,
∵AB=AE,
∴∠ABE=∠AEB,
∵AB=AE,
∴△ABA1≌△AEE1,
∴△ABA1与△AEE1属于一个全等类;
同理可得△ABE1≌△AEA1,△AA1E1≌△CB1C1,△ACD≌△CEA它们分别属于一个全等类.
∵△BC1E≌△ABE,
∴△ABC≌△AED,与△BC1E≌△ABE属于同一个全等类.
故图中不同全等类的个数为5个.
故选C.
点评:本题考查的是全等三角形的判定与正五边形的性质,根据题意得出不同种类的全等三角形是解答此题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
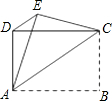 如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB=
如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB= 在直角坐标系xOy中,直线y=kx+3经过C(-2,1),交x轴、y轴分别于A、B两点.求不等式kx+3≥5x的解集.
在直角坐标系xOy中,直线y=kx+3经过C(-2,1),交x轴、y轴分别于A、B两点.求不等式kx+3≥5x的解集.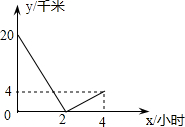 甲、乙二人从A、B两地同时出发相向而行,相遇后,甲立即返回,先于乙回到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,则乙从B地到A地需时间
甲、乙二人从A、B两地同时出发相向而行,相遇后,甲立即返回,先于乙回到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,则乙从B地到A地需时间