题目内容
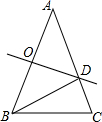 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④点D到线段BC的距离等于线段OD的长.
其中正确的是
考点:线段垂直平分线的性质,等腰三角形的性质
专题:常规题型
分析:根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°,则由∠C=2∠A;再根据线段的垂直平分线的性质得DA=DB,则∠DBA=∠A=36°,
所以∠DBA=∠DBC=36°;作DH⊥BC于H,根据角平分线的性质得DH=OD;利用三角形面积公式得到S△BOD=S△BDH.
所以∠DBA=∠DBC=36°;作DH⊥BC于H,根据角平分线的性质得DH=OD;利用三角形面积公式得到S△BOD=S△BDH.
解答: 解:∵∠A=36°,AB=AC,
解:∵∠A=36°,AB=AC,
∴∠ABC=∠C=
(180°-36°)=72°,
∴∠C=2∠A,所以①正确;
∵AB的垂直平分线OD交AB于点O,
∴DA=DB,
∴∠DBA=∠A=36°,
∴∠DBA=∠DBC=36°,即BD平分∠ABC,所以②正确;
作DH⊥BC于H,则DH=OD,OB=OH,所以④正确.
∴S△BOD=S△BDH,所以③错误;
故答案为①②④.
 解:∵∠A=36°,AB=AC,
解:∵∠A=36°,AB=AC,∴∠ABC=∠C=
| 1 |
| 2 |
∴∠C=2∠A,所以①正确;
∵AB的垂直平分线OD交AB于点O,
∴DA=DB,
∴∠DBA=∠A=36°,
∴∠DBA=∠DBC=36°,即BD平分∠ABC,所以②正确;
作DH⊥BC于H,则DH=OD,OB=OH,所以④正确.
∴S△BOD=S△BDH,所以③错误;
故答案为①②④.
点评:本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等.也考查了等腰三角形的性质和角平分线性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )
如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )A、y=
| ||
| B、y=2x+3 | ||
| C、y=3-x | ||
| D、y=x-3 |
要用三根小木棒摆成三角形,已经准备好了长度分别为10cm和18cm的两根小木棒,则第三根小木棒的长度可以是( )
| A、6cm | B、7cm |
| C、8cm | D、12cm |
 如图是二次函数y=ax2+bx+c的图象,有下列说法:
如图是二次函数y=ax2+bx+c的图象,有下列说法: