题目内容
 如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )
如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )A、y=
| ||
| B、y=2x+3 | ||
| C、y=3-x | ||
| D、y=x-3 |
考点:待定系数法求一次函数解析式
专题:计算题
分析:先利用正比例函数解析式确定B点坐标为(1,2),然后利用待定系数法求直线l的解析式.
解答:解:设直线l对应函数的表达式为y=kx+b,
把x=1代入y=2x得y=2,则B点坐标为(1,2),
把B(1,2),(0,3)代入y=kx+b得
,
解得
,
所以直线l对应函数的表达式为y=-x+3.
故选C.
把x=1代入y=2x得y=2,则B点坐标为(1,2),
把B(1,2),(0,3)代入y=kx+b得
|
解得
|
所以直线l对应函数的表达式为y=-x+3.
故选C.
点评:本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C的坐标分别为(1,0)、(6,0)、(8,5),则顶点D的坐标是( )
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C的坐标分别为(1,0)、(6,0)、(8,5),则顶点D的坐标是( )| A、(5,5) |
| B、(5,3) |
| C、(2,5 ) |
| D、(3,5) |
若点A(a+3,a+1)在直角坐标系的y轴上,则点A的坐标是( )
| A、(0,-2) |
| B、(2,0) |
| C、(4,0) |
| D、(0,-4) |
下列计算正确的是( )
| A、8+x=8x | ||
| B、3a2-a2=3 | ||
| C、6x2+2x3=8x5 | ||
D、
|
 如图,一次函数y=-
如图,一次函数y=-| 2 |
| 3 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
若a>b,则下列不等式成立的是( )
A、
| ||||
| B、a2>b2 | ||||
| C、2-a<2-b | ||||
| D、a-1<b-1 |
 如图,直线a∥b,把三角板的直角顶点放在直线b上,若∠1=60°,则∠2的度数为( )
如图,直线a∥b,把三角板的直角顶点放在直线b上,若∠1=60°,则∠2的度数为( )| A、45° | B、35° |
| C、30° | D、25° |
 如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,观察图形,甲、乙这四次成绩的方差S甲2、S乙2之间的大小关系是
如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,观察图形,甲、乙这四次成绩的方差S甲2、S乙2之间的大小关系是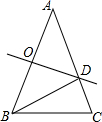 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论: