题目内容
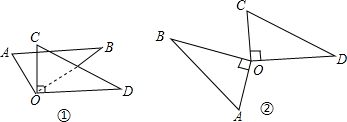
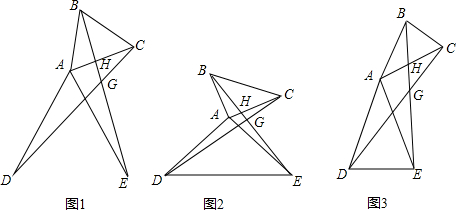
如图所示,两个相同的三角形有一个公共顶点,其中OA⊥OB,OC⊥OD,图中①、②分别是两个三角形有重叠部分和无重叠部分的两种放置状态.
(1)如图①,若∠BOC=60°,求∠AOD的度数;
(2)如图②,猜想∠AOD和∠BOC的大小关系,并写出理由.
(1)如图①,若∠BOC=60°,求∠AOD的度数;
(2)如图②,猜想∠AOD和∠BOC的大小关系,并写出理由.

考点:角的计算
专题:
分析:(1)由已知可先求出∠AOC,即可求出∠AOD的度数.
(2)利用周角与平角即可求出两角的关系.
(2)利用周角与平角即可求出两角的关系.
解答:解:(1)∵∠BOC=60°,OA⊥OB,
∴∠AOC=90°-60°=30°,
∴∠AOD=90°+30°=120°,
(2)∠AOD+∠BOC=180°,
∵OA⊥OB,OC⊥OD,
∴∠AOB+∠COD=180°,
∴∠AOD+∠BOC=360°-180°=180°.
∴∠AOC=90°-60°=30°,
∴∠AOD=90°+30°=120°,
(2)∠AOD+∠BOC=180°,
∵OA⊥OB,OC⊥OD,
∴∠AOB+∠COD=180°,
∴∠AOD+∠BOC=360°-180°=180°.
点评:本题主要考查了角的计算,解题的关键是灵活利用直角.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、实数与数轴上的点一一对应 |
| B、数轴上的点表示的数若不是有理数就是无理数 |
| C、有理数的运算及性质,在实数运算中仍成立 |
| D、对于实数a,若|a|=a,则a>0 |
下列各式中正确的是( )
A、-
| ||||
B、|-
| ||||
C、-
| ||||
D、-(-
|
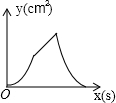
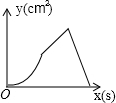
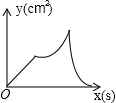
 如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )
如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )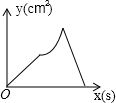
 如图,在四边形ABCD中,∠A=45°,∠C=90°,∠ABD=75°,∠DBC=30°,AB=2a,求BC的长.
如图,在四边形ABCD中,∠A=45°,∠C=90°,∠ABD=75°,∠DBC=30°,AB=2a,求BC的长.