题目内容
 如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )
如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )A、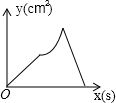 |
B、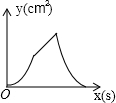 |
C、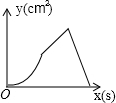 |
D、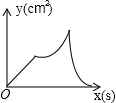 |
考点:动点问题的函数图象
专题:
分析:首先根据题意,运用分类讨论的数学思想求出y关于时间x的函数关系式,问题即可解决.
解答:解:设M,N第一次相遇时间为xs,
由题意得:2x+x=16,
解得x=
;
根据题意:
当点N在AD边,或在DC边上运动时,点M均在AB边上运动;
当点N在BC边上运动时,点M、N均在BC边上运动,直到相遇停止;
此时MN=4-(2x-8)-(x-4)=-3x+16
∴y=
,
故选C.
由题意得:2x+x=16,
解得x=
| 16 |
| 3 |
根据题意:
当点N在AD边,或在DC边上运动时,点M均在AB边上运动;
当点N在BC边上运动时,点M、N均在BC边上运动,直到相遇停止;
此时MN=4-(2x-8)-(x-4)=-3x+16
∴y=
|
故选C.
点评:该命题主要考查了动点问题的函数图象及其应用问题;解题的关键是准确把握题意,运用分类讨论的数学思想正确写出函数关系式.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图给出的是某月份的日历表,用小正方形方框任意框处相邻的四个数,请你用方程的思想来研究,发现这四个数的和可能是( )
如图给出的是某月份的日历表,用小正方形方框任意框处相邻的四个数,请你用方程的思想来研究,发现这四个数的和可能是( )| A、45 | B、50 | C、55 | D、60 |
 如图,求作△ABC的外接圆.
如图,求作△ABC的外接圆.
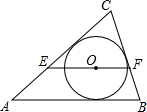 如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是