题目内容
如图1,已知等边△ABC和等边△ADE有一公共顶点A,连结BE、DC交于G,则有∠BGC=60°.
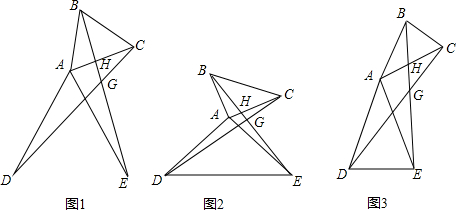
(1)请你证明这个结论;
(2)若△ABC和△ADE都为等腰直角三角形,如图2,观察图形,写出结论并加以证明;
(3)若△ABC和△ADE都为顶角是α的两个等腰三角形,如图3,你能得到什么结论?请写出这个结论;
(4)若△ABC和△ADE是顶角不相等的两个等腰三角形,还有与(3)相同结论成立吗?

(1)请你证明这个结论;
(2)若△ABC和△ADE都为等腰直角三角形,如图2,观察图形,写出结论并加以证明;
(3)若△ABC和△ADE都为顶角是α的两个等腰三角形,如图3,你能得到什么结论?请写出这个结论;
(4)若△ABC和△ADE是顶角不相等的两个等腰三角形,还有与(3)相同结论成立吗?
考点:全等三角形的判定与性质,等腰三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质得出AB=AC,AD=AE,∠ABC=∠ACB=60°,∠BAC=∠DAE,求出∠BAE=∠DAC,证出△BAE≌△CAD,推出∠ABE=∠ACD,求出∠BGC=180°-(∠ABC+∠ACB)即可;
(2)根据等边三角形的性质得出AB=AC,AD=AE,∠ABC=∠ACB=45°,∠BAC=∠DAE,求出∠BAE=∠DAC,证出△BAE≌△CAD,推出∠ABE=∠ACD,求出∠BGC=180°-(∠ABC+∠ACB)即可;
(3)根据等边三角形的性质得出AB=AC,AD=AE,∠BAC=∠DAE=α,求出∠BAE=∠DAC,证出△BAE≌△CAD,推出∠ABE=∠ACD,求出∠BGC=180°-(∠ABC+∠ACB)即可;
(4)根据已知不能推出∠ABE=∠ACD.
(2)根据等边三角形的性质得出AB=AC,AD=AE,∠ABC=∠ACB=45°,∠BAC=∠DAE,求出∠BAE=∠DAC,证出△BAE≌△CAD,推出∠ABE=∠ACD,求出∠BGC=180°-(∠ABC+∠ACB)即可;
(3)根据等边三角形的性质得出AB=AC,AD=AE,∠BAC=∠DAE=α,求出∠BAE=∠DAC,证出△BAE≌△CAD,推出∠ABE=∠ACD,求出∠BGC=180°-(∠ABC+∠ACB)即可;
(4)根据已知不能推出∠ABE=∠ACD.
解答:(1)证明:∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠ABC=∠ACB=60°,∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(60°+60°)
=60°;
(2)∠BGC=90°,
证明:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠ABC=∠ACB=45°,∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(45°+45°)
=90°;
(3)∠BGC=α,
理由是:∵△ABC和△ADE是都为顶角是α的两个等腰三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=α,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(180°-α)
=α;
(4)结论不成立,因为根据已知不能推出△BAE≌△CAD,即不能推出∠ABE=∠ACD.
∴AB=AC,AD=AE,∠ABC=∠ACB=60°,∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
|
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(60°+60°)
=60°;
(2)∠BGC=90°,
证明:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠ABC=∠ACB=45°,∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
|
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(45°+45°)
=90°;
(3)∠BGC=α,
理由是:∵△ABC和△ADE是都为顶角是α的两个等腰三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=α,
∴∠BAC+∠CAE=∠DAE+∠EAC,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
|
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∴∠BGC=180°-(∠EBC+∠DCA+∠ACB)
=180°-(∠EBC+∠EBA+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(180°-α)
=α;
(4)结论不成立,因为根据已知不能推出△BAE≌△CAD,即不能推出∠ABE=∠ACD.
点评:本题考查了等边三角形的性质,等腰直角三角形性质,等腰三角形的性质,全等三角形的性质和判定的应用,解此题的关键是推出∠ABE=∠ACD,题目比较好,难度偏大.

练习册系列答案
相关题目
在数轴上,与表示数-2的点的距离是3的点表示的数是( )
| A、1 | B、5 | C、±3 | D、1或-5 |
 如图,求作△ABC的外接圆.
如图,求作△ABC的外接圆.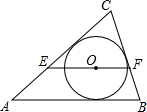 如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论: