题目内容
在△ABC中,∠B=30°,AB=6,AC=2
,求:
(1)BC的长;
(2)判定△ABC的形状.
| 3 |
(1)BC的长;
(2)判定△ABC的形状.
考点:解直角三角形
专题:
分析:(1)过A作AD⊥BC于D,分为两种情况,画出图形,求出BD和CD,即可求出答案;
(2)分别求出三边的平方,将两小边的平方和与最大边的平方进行比较,即可判断△ABC的形状.
(2)分别求出三边的平方,将两小边的平方和与最大边的平方进行比较,即可判断△ABC的形状.
解答: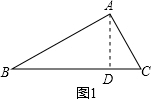 解:(1)如图1,过点A作AD⊥BC于点D,
解:(1)如图1,过点A作AD⊥BC于点D,
∵∠B=30°,AB=6,
∴AD=
AB=3,BD=AB•cos30°=6×
=3
.
在Rt△ACD中,∵AD=3,AC=2
,
∴DC=
=
=
,
 ∴BC=BD+DC=3
∴BC=BD+DC=3
+
=4
;
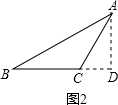
如图2,同理可得,
AD=
AB=3,BD=AB•cos30°=6×
=3
,DC=
=
=
,
∴BC=BD-DC=3
-
=2
.
综上所述,BC的长为4
或2
;
(2)如图1,在△ABC中,
∵AB=6,AC=2
,BC=4
,
∴AB2=36,AC2=12,BC2=48,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
如图2,在△ABC中,
∵AB=6,AC=2
,BC=2
,
∴AC=BC,即△ABC是等腰三角形,
又AB2=36,AC2=12,BC2=12,
∴BC2+AC2<AB2,
∴△ABC是钝角三角形;
综上所述,△ABC是直角三角形或等腰三角形.
 解:(1)如图1,过点A作AD⊥BC于点D,
解:(1)如图1,过点A作AD⊥BC于点D,∵∠B=30°,AB=6,
∴AD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
在Rt△ACD中,∵AD=3,AC=2
| 3 |
∴DC=
| AC2-AD2 |
| 12-9 |
| 3 |
 ∴BC=BD+DC=3
∴BC=BD+DC=3| 3 |
| 3 |
| 3 |
如图2,同理可得,
AD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| AC2-AD2 |
| 12-9 |
| 3 |
∴BC=BD-DC=3
| 3 |
| 3 |
| 3 |
综上所述,BC的长为4
| 3 |
| 3 |
(2)如图1,在△ABC中,
∵AB=6,AC=2
| 3 |
| 3 |
∴AB2=36,AC2=12,BC2=48,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
如图2,在△ABC中,
∵AB=6,AC=2
| 3 |
| 3 |
∴AC=BC,即△ABC是等腰三角形,
又AB2=36,AC2=12,BC2=12,
∴BC2+AC2<AB2,
∴△ABC是钝角三角形;
综上所述,△ABC是直角三角形或等腰三角形.
点评:本题考查了解直角三角形,勾股定理及其逆定理的应用,主要考查学生的计算能力,进行分类讨论是解题的关键.

练习册系列答案
相关题目
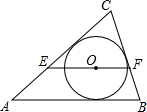 如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
 如图,A为⊙O外的一点,OA交⊙O于点C,AB是⊙O的切线,B是切点,∠A=30°,
如图,A为⊙O外的一点,OA交⊙O于点C,AB是⊙O的切线,B是切点,∠A=30°,