Question

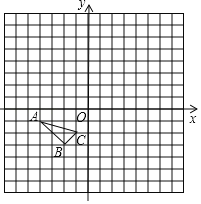
【题目】如图在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．

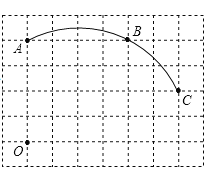
（1）请完成如下操作：

①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；　②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．

（2）请在（1）的基础上，完成下列填空：

①写出点的坐标：C 、D ；

②⊙D的半径= （结果保留根号）；

③若E（7，0），试判断直线EC与⊙D的位置关系，并说明你的理由．

Answer 1

【答案】（1）见解析；（2）①根据图形得：C（6，2），D（2，0）；②；③CE与⊙D相切，理由见解析

【解析】

（1）根据题意建立平面直角坐标系，然后作出弦AB的垂直平分线，以及BC的垂直平分线，两直线的交点即为圆心D，连接AD，CD；

（2）①根据第一问画出的图形即可得出C及D的坐标；

②在直角三角形AOD中，由OA及OD的长，利用勾股定理求出AD的长，即为圆O的半径；

③直线CE与圆O的位置关系是相切，理由为：由圆的半径得出DC的长，在直角三角形CEF中，由CF及FE的长，利用勾股定理求出CE的长，再由DE的长，利用勾股定理的逆定理得出三角形DCE为直角三角形，即EC垂直于DC，可得出直线CE为圆O的切线．

（1）根据题意画出相应的图形，如下图所示：

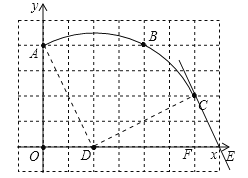
（2）①根据图形得：C（6，2），D（2，0）；

②∵OD=2，OA=4,

由勾股定理得，AD==

③直线EC与⊙D的位置关系为相切，理由为：

在Rt△CEF中，CF=2，EF=1，

根据勾股定理得：CE==

在△CDE中，CD=，CE=，DE=5，

∵CE2+CD2=（）2+（）2=5+20=25，DE2=25，

∴CE2+CD2=DE2，

∴△CDE为直角三角形，即∠DCE=90°，

∴CE⊥DC，

则CE与⊙D相切．