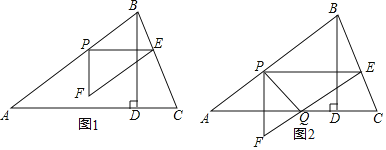ЬтФПФкШн
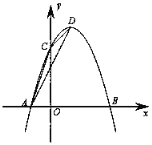
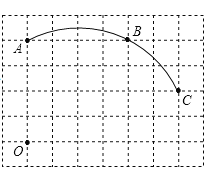
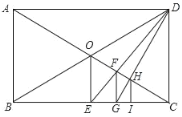
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌАбвдИёЕуЮЊЖЅЕуЕФШ§НЧаЮГЦЮЊИёЕуШ§НЧаЮЃЈУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ЕФе§ЗНаЮЃЉЃЎЭМжаЁїABCЪЧИёЕуШ§НЧаЮЃЌЕуAЃЌBЃЌCЕФзјБъЗжБ№ЪЧЃЈЉ4ЃЌЉ1ЃЉЃЌЃЈЉ2ЃЌЉ3ЃЉЃЌЃЈЉ1ЃЌЉ2ЃЉЃЎ
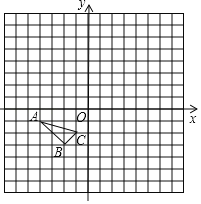
ЃЈ1ЃЉвдOЮЊа§зЊжааФЃЌАбЁїABCШЦOЕуЫГЪБеыа§зЊ90ЁуКѓЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉвдOЮЊЮЛЫЦжааФЃЌдкЕквЛЯѓЯоФкАбЁїABCЗХДѓ2БЖКѓЕУЕНЁїA2B2C2ЃЌЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉЁїABCФкгавЛЕуPЃЈaЃЌbЃЉЃЌаДГіОЙ§ЃЈ2ЃЉЮЛЫЦБфЛЛКѓPЕФЖдгІЕуP1ЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉШчЭМЃЌЁїA1B1C1ЮЊЫљзїЃЛМћНтЮіЃЛЃЈ2ЃЉШчЭМЃЌЁїA2B2C2ЮЊЫљзїЃЛМћНтЮіЃЛЃЈ3ЃЉЕуPЕФЖдгІЕуP1ЕФзјБъЮЊЃЈЉ2aЃЌЉ2bЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЭјИёЬиЕуКЭа§зЊЕФаджЪвРДЮзїГіЕуAЁЂBЁЂCЕФЖдгІЕуA1ЁЂB1ЁЂC1ЕФзјБъЃЌдйЫГДЮСЌНгМДПЩЃЛ
ЃЈ2ЃЉАбЕуAЁЂBЁЂCЕФКсзнзјБъЖМГЫвдЃ2ЕУЕНЕуA2ЁЂB2ЁЂC2ЕФзјБъЃЌдйЫГДЮСЌНгМДПЩЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЬтЖдгІЕуЕФзјБъЬиЕуЧѓНт.
ЃЈ1ЃЉШчЭМЃЌЁїA1B1C1ЮЊЫљзїЃЛ
ЃЈ2ЃЉШчЭМЃЌЁїA2B2C2ЮЊЫљзїЃЛ

ЃЈ3ЃЉЕуPЕФЖдгІЕуP1ЕФзјБъЮЊЃЈЉ2aЃЌЉ2bЃЉЃЎ