题目内容
2．
如图，在网格内有一直角三角形ABC，请把三角形先向右平移2个单位，再向下平移3个单位，得到三角形A′B′C′，请画出平移后的三角形A′B′C′，并计算AA′的长．
分析 利用网格特点和平移的方向与距离分别画出点A、B、C的对应点A′、B′、C′．从而得到△A′B′C′，然后利用勾股定理计算AA′的长．
解答 解：如图，△A′B′C′为所作；
AA′=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$．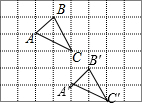
点评 本题考查了作图-平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
练习册系列答案
相关题目
12．
如图，将四边形ABCD先向左平移2个单位长度，再向上平移1个单位长度，那么点B的对应点B′的坐标是（ ）
如图，将四边形ABCD先向左平移2个单位长度，再向上平移1个单位长度，那么点B的对应点B′的坐标是（ ）| A． | （4，-1） | B． | （-4，-1） | C． | （4，1） | D． | （5，1） |
下面是某医院各部门的示意图，横向表示的是楼层，纵向表示的是门号，例如：院长室在4楼3门，我们用（4，3）来表示其位置，试根据上面方法，结合图形，完成下面问题：
在平面直角坐标系中，点A的坐标是（0，3），点B的坐标是（-4，0），将△AOB绕点A逆时针旋转90°得到△AEF，点O、B的对应点分别是点E、F．
7．下列叙述中，正确的是（ ）
| A． | 在同一平面内，两条直线的位置关系有三种，分别是相交、平行、垂直 | |
| B． | 不相交的两条直线叫平行线 | |
| C． | 两条直线的铁轨是平行的 | |
| D． | 我们知道，对顶角是相等的，那么反过来，相等的角就是对顶角 |
如图，三角形ABC在平面直角坐标系中．
11．
如图，能判定AD∥BC的条件是（ ）
如图，能判定AD∥BC的条件是（ ）| A． | ∠3=∠2 | B． | ∠1=∠2 | C． | ∠B=∠D | D． | ∠B=∠1 |