题目内容
18.化简:(1)3x2-y2-3x2-5y+x2-5y+y2
(2)$\frac{1}{3}(3{x^2}-y)-\frac{2}{3}(2{x^2}+y)$.
分析 结合整式加减法的运算法则进行求解即可.
解答 解:(1)3x2-y2-3x2-5y+x2-5y+y2
=x2-10y.
(2)$\frac{1}{3}(3{x^2}-y)-\frac{2}{3}(2{x^2}+y)$
=x2-$\frac{1}{3}$y-$\frac{4}{3}$x2-$\frac{2}{3}$y
=$-\frac{1}{3}{x^2}-y$.
点评 本题考查了整式的加减,解答本题的关键在于熟练掌握整式加减法的运算法则.

练习册系列答案
相关题目
19.已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
(1)根据上表填空:
①这个抛物线的对称轴是x=1,抛物线一定会经过点(-2,10 );
②抛物线在对称轴右侧部分是上升(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
| x | … | -1 | 0 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 2 | 5 | 10 | … |
①这个抛物线的对称轴是x=1,抛物线一定会经过点(-2,10 );
②抛物线在对称轴右侧部分是上升(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
 把图中的等边三角形分成2个、3个、4个全等图形.
把图中的等边三角形分成2个、3个、4个全等图形.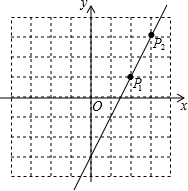 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.