题目内容
13．已知5x2-2xy+y2+4x+1=0，求x，y的值．分析 首先把5x2-2xy+y2+4x+1=0变为x2-2xy+4x2+4x+1=0，然后利用完全平方公式变为两个非负数的和，最后利用非负数的性质即可求解．
解答 解：∵5x2-2xy+y2+4x+1=x2-2xy+y2+4x2+4x+1=（x-y）2+（2x+1）2=0，
∴x-y=0且2x+1=0，
解得x=-$\frac{1}{2}$，y=-$\frac{1}{2}$．
点评 本题考查了配方法的应用和非负数的性质，几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
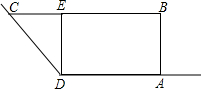某农场拟建一个梯形饲养场ABCD，其中AD，CD分别靠现有墙DM，DN，其余用新墙砌成，墙DM长为9米，墙DN足够长，两面墙形成的角度为135°，新墙DE将饲养场隔成△CDE和矩形ABED两部分．已知新建墙体总长为30米．设AB=x米，梯形饲养场ABCD的面积为S米2．
2．下列计算正确的是（ ）
| A． | （-3）2=-9 | B． | （-2）2=-10 | C． | （-$\frac{1}{2}$）3=-$\frac{1}{8}$ | D． | -3+$\frac{2}{3}$=-3$\frac{2}{3}$ |