题目内容
10.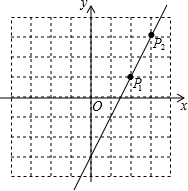 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.(1)求直线l所表示的一次函数的表达式;
(2)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.
分析 (1)设直线l所表示的一次函数的表达式为y=kx+b(k≠0),把点P1、P2的坐标代入,利用待定系数法求得系数的值;
(2)根据平移的规律得到点P3的坐标为(6,9),代入直线方程进行验证即可.
解答 解:(1)设直线l所表示的一次函数的表达式为y=kx+b(k≠0),
∵点P1(2,1),P2(3,3)在直线l上,
∴$\left\{\begin{array}{l}{2k+b=1}\\{3k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-3}\end{array}\right.$.
∴直线l所表示的一次函数的表达式为y=2x-3.
(2)点P3在直线l上.
由题意知点P3的坐标为(6,9),
∵2×6-3=9,
∴点P3在直线l上.
点评 本题考查了待定系数法求一次函数解析式,坐标与图形变化-平移.根据平移的规律求得点P2、P3的坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列计算正确的是( )
| A. | (-3)2=-9 | B. | (-2)2=-10 | C. | (-$\frac{1}{2}$)3=-$\frac{1}{8}$ | D. | -3+$\frac{2}{3}$=-3$\frac{2}{3}$ |
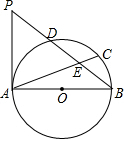 如图所示,AB为⊙O的直径,D为$\widehat{AC}$的中点,AC、BD交于点E,P为BD延长线上一点,且PD=DE.
如图所示,AB为⊙O的直径,D为$\widehat{AC}$的中点,AC、BD交于点E,P为BD延长线上一点,且PD=DE.