题目内容
6.已知x1,x2是方程x2+x-3=0的两个实数根,求以${x}_{1}^{2}$和${x}_{2}^{2}$为根的一元二次方程.分析 根据根与系数的关系得到x1+x2=-1,x1x2=-3,再利用完全平方公式得到${x}_{1}^{2}$+${x}_{2}^{2}$=(x1+x2)2-2x1x2,${x}_{1}^{2}$${x}_{2}^{2}$,然后利用整体代入的方法计算得出数值,进一步得出方程即可.
解答 解:∵x1,x2是方程x2+x-3=0的两个实数根,
∴x1+x2=-1,x1x2=-3,
∴${x}_{1}^{2}$+${x}_{2}^{2}$=(x1+x2)2-2x1x2=7,${x}_{1}^{2}$${x}_{2}^{2}$=9,
∴以${x}_{1}^{2}$和${x}_{2}^{2}$为根的一元二次方程为x2-7x+9=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,△ABC中,OF是AB的垂直平分线,垂足为F,OA=OC,求证:点O在线段BC的垂直平分线上.
如图,△ABC中,OF是AB的垂直平分线,垂足为F,OA=OC,求证:点O在线段BC的垂直平分线上. 如图是小明做的一个风筝的支架,AB=40cm,BP=60cm,BC=30cm,且△ABC与△APQ相似,求PQ的长.
如图是小明做的一个风筝的支架,AB=40cm,BP=60cm,BC=30cm,且△ABC与△APQ相似,求PQ的长. 数a、b、c在数轴上的对应位置如图所示:把下列各组数按从小到大的顺序排列,并用“<”连接起来:
数a、b、c在数轴上的对应位置如图所示:把下列各组数按从小到大的顺序排列,并用“<”连接起来: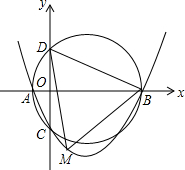 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C的圆与y轴的另一个交点为D.已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4).
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C的圆与y轴的另一个交点为D.已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4).