题目内容
1.已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.(1)【特殊情况,探索结论】
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE=DB(填“>”、“<”或“=”).
(2)【特例启发,解答题目】
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE=DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程).
(3)【拓展结论,设计新题】
在等边三角形ABC中,点E在直线AB上,点D在直线CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长(请你画出相应图形,并直接写出结果).
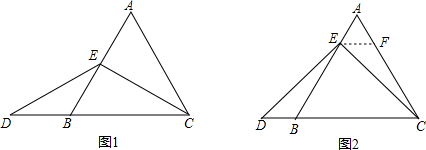
分析 (1)由E为等边三角形AB边的中点,利用三线合一得到CE垂直于AB,且CE为角平分线,由ED=EC,利用等边对等角及等腰三角形的性质得到一对角相等,利用等角对等边即可得证;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,由三角形ABC为等边三角形,得到三角形AEF为等边三角形,进而得到AE=EF=AF,BE=FC,再由ED=EC,以及等式的性质得到夹角相等,利用SAS得到三角形BDE与三角形EFC全等,利用全等三角形对应边相等得到DB=EF,等量代换即可得证;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,由BC+DB求出CD的长即可.
解答 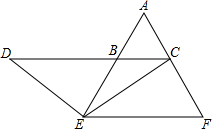 解:(1)当E为AB的中点时,AE=DB;
解:(1)当E为AB的中点时,AE=DB;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°-∠D,∠ECF=60°-∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,
$\left\{\begin{array}{l}{DE=CE}\\{∠DEB=∠ECF}\\{BE=FC}\end{array}\right.$,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=
点评 此题考查了等边三角形的判定与性质,全等三角形的判定与性质,以及等腰三角形的性质,熟练掌握等边三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
16.若α为锐角,且sinα=$\frac{4}{5}$,则tanα为( )
| A. | $\frac{9}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
10.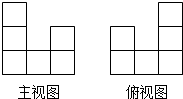 如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
 如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )| A. | 11个 | B. | 12个 | C. | 13个 | D. | 14个 |
11.若M(-$\frac{1}{2}$,y1)、N(-$\frac{1}{4}$,y2)、P($\frac{1}{2}$,y3)三点都在函数y=-$\frac{1}{x}$的图象上,则y1、y2、y3的大小关系为( )
| A. | y2>y3>y1 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |