题目内容
20.(1)化简:($\frac{{a}^{2}+2a}{a}-1$)÷$\frac{{a}^{2}-1}{2}$;(2)先化简,再求值:$\frac{3-m}{2m-4}÷(m+2-\frac{5}{m-2})$,其中m=-4.
分析 (1)直接根据分式混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把m的值代入进行计算即可.
解答 解:(1)原式=$\frac{{a}^{2}+2a-a}{a}$•$\frac{2}{(a+1)(a-1)}$
=(a+1)•$\frac{2}{(a+1)(a-1)}$
=$\frac{2}{a-1}$;
(2)原式=$\frac{3-m}{2(m-2)}$÷$\frac{{m}^{2}-4-5}{m-2}$
=$\frac{3-m}{2(m-2)}$÷$\frac{{m}^{2}-9}{m-2}$
=$\frac{3-m}{2(m-2)}$•$\frac{m-2}{(m+3)(m-3)}$
=-$\frac{1}{2(m+3)}$,
当m=-4时,原式=-$\frac{1}{2(-4+3)}$=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列两个整式中,是同类项的是( )
| A. | 2a3b和2ab3 | B. | abc和bcd | C. | 4x和4y | D. | -2x2y2和5x2y2 |
9. 如图中字母A所代表的正方形的面积为( )
如图中字母A所代表的正方形的面积为( )
 如图中字母A所代表的正方形的面积为( )
如图中字母A所代表的正方形的面积为( )| A. | 12 | B. | 5 | C. | 10 | D. | 25 |
10.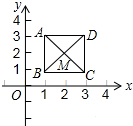 如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
 如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2012,2) | B. | (-2012,-2) | C. | (-2013,-2) | D. | (-2013,2) |
 已知不等式组$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$,
已知不等式组$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$, 要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环)
要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环) 一个几何体由几个大小相同的小立方块搭成,如图分别给出了从正面、左面、上面看到的几何体的形状图,则搭成这个几何体的小立方块的个数是( )
一个几何体由几个大小相同的小立方块搭成,如图分别给出了从正面、左面、上面看到的几何体的形状图,则搭成这个几何体的小立方块的个数是( ) 如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.
如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.