题目内容
6.已知k>1,b=k,a+c=2k2,ac=2k4-$\frac{1}{2}$k2,则以a,b,c为边的三角形是( )| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 无法确定 |
分析 根据根与系数的关系得出a,b的值,进而得出a2+c2=k2=b2,即可得出答案.
解答 解:∵a+c=2k2,ac=2k4-$\frac{1}{2}$k2,
∴a,c可以认为是x2-(2k2)x+2k4-$\frac{1}{2}$k2=0的两根,
解得:x1=$\frac{2{k}^{2}+\sqrt{-4{k}^{4}+2{k}^{2}}}{2}$,x2=$\frac{2{k}^{2}-\sqrt{-4{k}^{4}+2{k}^{2}}}{2}$,
∵b=k,
∴b2=k2,
不妨令a=$\frac{2{k}^{2}+\sqrt{-4{k}^{4}+2{k}^{2}}}{2}$,c=$\frac{2{k}^{2}-\sqrt{-4{k}^{4}+2{k}^{2}}}{2}$,
于是a2+c2=k2=b2,
即b2=a2+c2,故为直角三角形.
故选:C.
点评 此题主要考查了根与系数的关系以及勾股定理的逆定理,根据已知得出a,c的值是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
17.计算:-(-1)=( )
| A. | 1 | B. | -1 | C. | -2 | D. | ±1 |
 已知:如图,BE与CF相交于点G.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
已知:如图,BE与CF相交于点G.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.

 如图,在?ABCD中,AE⊥BC于E,AF⊥DC于F,∠ADC=60°,BE=2,CF=1,求?ABCD的面积.
如图,在?ABCD中,AE⊥BC于E,AF⊥DC于F,∠ADC=60°,BE=2,CF=1,求?ABCD的面积.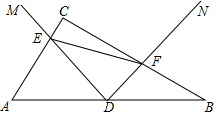 如图,△ABC中,∠ACB=90°,点D是AB中点,∠MDN=90°,DM交AC于点E,DN交BC于点F.
如图,△ABC中,∠ACB=90°,点D是AB中点,∠MDN=90°,DM交AC于点E,DN交BC于点F.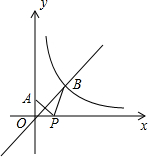 如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y=$\frac{{k}^{2}}{x}$(k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是3.
如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y=$\frac{{k}^{2}}{x}$(k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是3.