题目内容
16.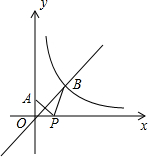 如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y=$\frac{{k}^{2}}{x}$(k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是3.
如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y=$\frac{{k}^{2}}{x}$(k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是3.
分析 首先解直线y=x与反比例函数解析式组成的方程组,求得B的坐标,然后求得A关于x轴的对称点坐标,PA+PB的最小值就是A的对称点与B之间的距离,据此列方程求得k的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{y=x}\\{y=\frac{{k}^{2}}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=k}\\{y=k}\end{array}\right.$或$\left\{\begin{array}{l}{x=-k}\\{y=-k}\end{array}\right.$(舍去),则B的坐标是(k,k).
A关于x轴的对称点是(0,-1).
则根据题意得k2+(k+1)2=52,
解得:k=3或-4(舍去).
故答案是:3.
点评 本题考查了轴对称的应用,理解PA+PB的值最小的条件是关键.

练习册系列答案
相关题目
6.已知k>1,b=k,a+c=2k2,ac=2k4-$\frac{1}{2}$k2,则以a,b,c为边的三角形是( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 无法确定 |
11.下列等式一定成立的是( )
| A. | 2a+3b=5ab | B. | (a3)2=a5 | C. | a2•a3=a5 | D. | (a+b)2=a2+b2 |
1.义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
| A. | 3.5×108 | B. | 3.5×109 | C. | 35×108 | D. | 0.35×109 |
6.下列方程是一元二次方程的是( )
| A. | 9x2-5x=9 | B. | 4x+8=0 | C. | 6x3+8x-1=0 | D. | x2-$\frac{1}{x}$=6 |
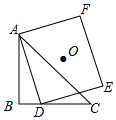 如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$.
如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$.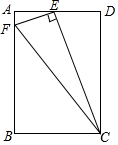 如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,△AEF与△DCE是否相似?请加以说明.
如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,△AEF与△DCE是否相似?请加以说明. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.