题目内容
20．不等式组$\left\{\begin{array}{l}{x-a＞0}\\{x-b＜0}\end{array}\right.$的解集是-a＜x＜b，则不等式组$\left\{\begin{array}{l}{x-a＜0}\\{x+b＞0}\end{array}\right.$的解集是-b＜x＜a．分析 根据不等式的性质证得x-a＜x+b．然后解不等式组．
解答 解：∵不等式组$\left\{\begin{array}{l}{x-a＞0}\\{x-b＜0}\end{array}\right.$的解集是-a＜x＜b，
∴x-a＜x+b．
∴不等式组$\left\{\begin{array}{l}{x-a＜0}\\{x+b＞0}\end{array}\right.$的解集是：-b＜x＜a．
故答案是：-b＜x＜a．
点评 本题考查的是一元一次不等式组的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
阅读快车系列答案
相关题目
10．函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是（ ）
| A． | k＜3 | B． | k＜3且k≠0 | C． | k≤3且k≠0 | D． | k≤3 |
11．下列计算中，正确的是（ ）
| A． | 2a+3b=5ab | B． | （3a3）2=6a6 | C． | a6+a2=a3 | D． | -3a+2a=-a |
15．
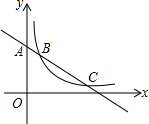如图，直线y=-$\frac{\sqrt{3}}{3}$x+b与y轴交于点A，与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点，且AB•AC=4，则k=（ ）
如图，直线y=-$\frac{\sqrt{3}}{3}$x+b与y轴交于点A，与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点，且AB•AC=4，则k=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
9．∠1和∠2是对顶角的图形为（ ）
| A． |  | B． |  | C． |  | D． |  |
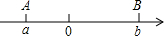阅读下面材料：点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．回答下列问题：