题目内容
17. 如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是$\sqrt{2}$π.
如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是$\sqrt{2}$π.
分析 如图点P运动的路径是以G为圆心的弧$\widehat{EF}$,在⊙G上取一点H,连接EH、FH,只要证明∠EGF=90°,求出GE的长即可解决问题.
解答 解:如图点P运动的路径是以G为圆心的弧$\widehat{EF}$,在⊙G上取一点H,连接EH、FH.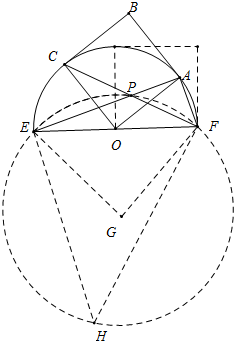
∵四边形AOCB是正方形,
∴∠AOC=90°,
∴∠AFP=$\frac{1}{2}$∠AOC=45°,
∵EF是⊙O直径,
∴∠EAF=90°,
∴∠APF=∠AFP=45°,
∴∠EPF=135°,
∵EF是定值,
∴点P在以点G为圆心,GE为半径的圆上,
∴∠H=∠APF=45°,
∴∠EGF=2∠H=90°,
∵EF=4,GE=GF,
∴EG=GF=2$\sqrt{2}$,
∴$\widehat{EF}$的长=$\frac{90π•2\sqrt{2}}{180}$=$\sqrt{2}$π.
故答案为$\sqrt{2}$π.
点评 本题考查正方形的性质、旋转的性质、轨迹、圆等知识,解题的关键是正确发现轨迹的位置,学会添加辅助线,利用圆的有关性质解决问题,属于中考填空题中的压轴题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
8.某工厂计划每天生产x吨生产资料,采用新技术后每天多生产3吨,实际生产180吨与原计划生产120吨的时间相等,那么适合x的方程是( )
| A. | $\frac{120}{x+3}=\frac{180}{x}$ | B. | $\frac{120}{x-3}=\frac{180}{x}$ | C. | $\frac{120}{x}=\frac{180}{x+3}$ | D. | $\frac{120}{x}=\frac{180}{x-3}$ |
5.下列命题中,不正确的是( )
| A. | 有一个角是60°的等腰三角形是等边三角形 | |
| B. | 一组对边平行且一组对角相等的四边形是平行四边形 | |
| C. | 对角线互相垂直且相等的四边形是矩形 | |
| D. | 对角线相等的菱形是正方形 |
2.某公司去年的利润(总产值-总支出)为200万元.今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.如果去年的总产值x万元、总支出y万元,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=200}\\{(1+20%)x-(1-10%)y=780}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=200}\\{(1-20%)x-(1+10%)y=780}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y=200}\\{20%x-10%y=780}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=200}\\{(1-20%)x-(1-10%)y=780}\end{array}\right.$ |
9.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=20 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=20 | C. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{3}$ | D. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{3}$ |
6. 如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
 如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )| A. | PC⊥OA,PD⊥OB | B. | OC=OD | C. | ∠OPC=∠OPD | D. | PC=PD |