题目内容
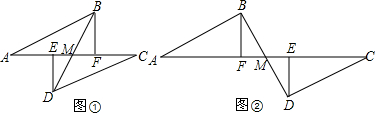
如图①,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB=CD.
(1)求证:BM=DM;
(2)若将△DEC的边EC沿AC方向移动至如图②所示的位置时,其余条件不变,上述结论是否成立?请说明理由.
(1)求证:BM=DM;
(2)若将△DEC的边EC沿AC方向移动至如图②所示的位置时,其余条件不变,上述结论是否成立?请说明理由.

考点:全等三角形的判定与性质
专题:常规题型
分析:(1)根据题干中给出的条件可以证明△ABF≌△CDE,可以证明BF=DE,即可证明△BFN≌△DEM,可得BM=DM;
(2)求证方法和(1)相同.
(2)求证方法和(1)相同.
解答:解:(1)∵AE=CF,AF=AE+EF,CE=CF+EF
∴AF=CE,∵DE⊥AC,BF⊥AC,∴△ABF、△CDE为直角三角形,
在RT△ABF和RT△CDE中,
,
∴△ABF≌△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
,
∴△DEM≌△BFM(AAS),
∴BM=DM.
(2)成立,求证如下:
∵AE=CF,AF=AE+EF,CE=CF+EF
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴△ABF、△CDE为直角三角形,
在RT△ABF和RT△CDE中,
,
∴△ABF≌△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
,
∴△DEM≌△BFM(AAS),
∴BM=DM.
∴AF=CE,∵DE⊥AC,BF⊥AC,∴△ABF、△CDE为直角三角形,
在RT△ABF和RT△CDE中,
|
∴△ABF≌△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
|
∴△DEM≌△BFM(AAS),
∴BM=DM.
(2)成立,求证如下:
∵AE=CF,AF=AE+EF,CE=CF+EF
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴△ABF、△CDE为直角三角形,
在RT△ABF和RT△CDE中,
|
∴△ABF≌△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
|
∴△DEM≌△BFM(AAS),
∴BM=DM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证BF=DE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x2+2x-4=0的两根为x1,x2,则x1+x2的值为( )
| A、2 | B、-2 | C、4 | D、-4 |
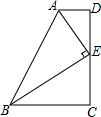 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,且BE⊥AE,求证:AB=BC+AD.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,且BE⊥AE,求证:AB=BC+AD.
 如图,C是AB的中点,∠ECA=∠DCB,CD=CE,∠A=40°,求∠B的度数.
如图,C是AB的中点,∠ECA=∠DCB,CD=CE,∠A=40°,求∠B的度数. 如图,AB=AD,CB=CD,说明:AC平分
如图,AB=AD,CB=CD,说明:AC平分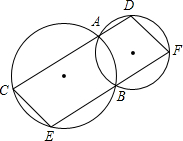 如图,两圆相交于A,B两点,直线CD过点A交两圆于C,D,直线EF交两圆于E,F.探索CE,DF的位置关系.
如图,两圆相交于A,B两点,直线CD过点A交两圆于C,D,直线EF交两圆于E,F.探索CE,DF的位置关系. 如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.
如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.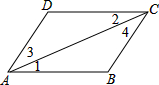 请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么?
请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么?