题目内容
11.某校在开展“校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果购买两种款式的书包共80个,那么女款书包最多能买多少个?
分析 (1)设原计划买男款书包x个,则女款书包(60-x)个,根据题意得:50x+70(60-x)=3400,即可解答;
(2)设女款书包能买y个,则男款书包(80-y)个,根据题意得:70y+50(80-y)≤4800,即可解答.
解答 解:(1)设原计划买男款书包x个,则女款书包(60-x)个,
根据题意得:50x+70(60-x)=3400,
解得:x=40,
60-x=60-40=20,
答:原计划买男款书包40个,则女款书包20个.
(2)设女款书包能买y个,则男款书包(80-y)个,
根据题意得:70y+50(80-y)≤4800,
解得:y≤40,
∴女款书包最多能买40个.
点评 本题考查了一元一次方程、一元一次不等式的应用,解决本题的关键是根据题意列出方程和不等式.

练习册系列答案
相关题目
19.关于x的一元二次方程x2+x+m=0有实数根,则m的取值范围是( )
| A. | m≥$-\frac{1}{4}$ | B. | m≤$-\frac{1}{4}$ | C. | m≥$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
 由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )
由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )



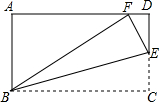 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为$\frac{5}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为$\frac{5}{3}$. 如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF.
如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF.