题目内容
 如图,Rt△ABC中∠C=90°,AD•AC=AE•AB,求证:DE⊥AB.
如图,Rt△ABC中∠C=90°,AD•AC=AE•AB,求证:DE⊥AB.考点:相似三角形的判定与性质
专题:证明题
分析:把乘积式转化为
=
,再根据两边对应成比例,夹角相等的两三角形相似证明△ABC和△ADE相似,然后根据相似三角形对应边成比例可得∠AED=∠C,再利用垂直的定义证明即可.
| AD |
| AB |
| AE |
| AC |
解答:证明:∵AD•AC=AE•AB,
∴
=
,
∵∠DAE=∠BAC,
∴△ABC∽△ADE,
∴∠AED=∠C=90°,
∴DE⊥AB.
∴
| AD |
| AB |
| AE |
| AC |
∵∠DAE=∠BAC,
∴△ABC∽△ADE,
∴∠AED=∠C=90°,
∴DE⊥AB.
点评:本题考查了相似三角形的判定与性质,熟练掌握三角形相似的判定方法并把乘积式转化成比例式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,数轴的单位长度为1,如果B、C表示的数的和为2,那么A、D表示的数的和是( )
如图,数轴的单位长度为1,如果B、C表示的数的和为2,那么A、D表示的数的和是( )| A、5 | B、4 | C、3 | D、2 |
在-3,0,-2,-
四个数中最小的是( )
| 2 |
| A、-3 | ||
| B、0 | ||
| C、-2 | ||
D、-
|
 用字母表示如图长方形中空白部分的面积.(要求列示并化简)
用字母表示如图长方形中空白部分的面积.(要求列示并化简) 小明用纸(如图)折成一个正方体的盒子,里面装入礼物,混放在下面的盒子里,请观察,礼物所在的盒子是( )
小明用纸(如图)折成一个正方体的盒子,里面装入礼物,混放在下面的盒子里,请观察,礼物所在的盒子是( )



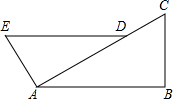 已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.
已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.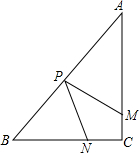 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).