Question

9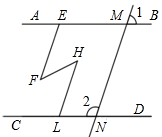．已知：如图，∠1+∠2=180°，∠AEF=∠HLN，判断图中有哪些直线平行，并给予证明．

Answer 1

分析 利用对顶角相等得到∠1=∠AMN，则∠1+∠AMN=180°，于是根据同旁内角互补，两直线平行可判断AB∥CD；延长EF交CD与G，如图，由AB∥CD得到∠AEG=∠EGN，加上∠AEF=∠HLN，所以∠EGN=∠HLN，于是根据同位角相等，两直线平行可判断EF∥HL．

解答 解：AB∥CD，EF∥HL．理由如下：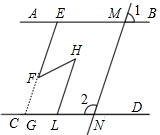
∵∠1=∠AMN，
∵∠1+∠2=180°，
∴∠1+∠AMN=180°，
∴AB∥CD；
延长EF交CD与G，如图，
∵AB∥CD，
∴∠AEG=∠EGN，
∵∠AEF=∠HLN，
∴∠EGN=∠HLN，
∴EF∥HL．

点评 本题考查了平行线的判定：同位角相等，两直线平行；同旁内角互补，两直线平行；内错角相等，两直线平行．