题目内容
在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3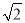 ,BC=5,求AC的长;
,BC=5,求AC的长;
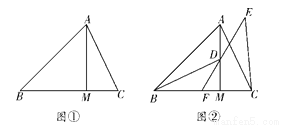
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
题目内容
在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3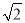 ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案