题目内容
【题目】在平面直角坐标系中，点
，
，过第四象限内一动点
作
轴的垂线，垂足为
，且
，点
、
分别在线段
和
轴上运动，则
的最小值是（ ）
A.
B.
C.
D.
【答案】B
【解析】
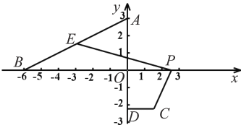
先求出直线AB的解析式，再根据已知条件求出点C的运动轨迹，由一次函数的图像及性质可知：点C的运动轨迹和直线AB平行，过点C作CE⊥AB交x轴于P，交AB于E，过点M（0，-3）作MN⊥AB于N根据垂线段最短和平行线之间的距离处处相等，可得此时CE即为
的最小值，且MN=CE，然后利用锐角三角函数求MN即可求出CE.
解：设直线AB的解析式为y=ax＋b（a≠0）
将点
，
代入解析式，得
解得：
∴直线AB的解析式为
设C点坐标为（x，y）
∴CD=x，OD=-y
∵
∴
整理可得：
，即点C的运动轨迹为直线的一部分
由一次函数的性质可知：直线和直线平行，
过点C作CE⊥AB交x轴于P，交AB于E，过点M（0，-3）作MN⊥AB于N根据垂线段最短和平行线之间的距离处处相等，可得此时CE即为的最小值，且MN=CE，如图所示
在Rt△AOB中，AB=
，sin∠BAO=
在Rt△AMN中，AM=6，sin∠MAN=
∴CE=MN=
，即的最小值是.
故选：B.
练习册系列答案
相关题目
