Question

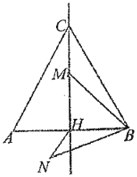
【题目】如图，等边三角形的边长是2，是高所在直线上的一个动点，连接，将线段绕点逆时针旋转得到，连接，则在点运动过程中，线段长度的最小值是（ ）

A.B.1C.D.

Answer 1

【答案】B

【解析】

由旋转的特性以及∠MBN＝60°，可知△BMN是等边三角形，从而得出MN＝BN，再由点到直线的所有线段中，垂线段最短可得出结论．

解：由旋转的特性可知，BM＝BN，
又∵∠MBN＝60°，
∴△BMN为等边三角形．
∴MN＝BM，
∵点M是高CH所在直线上的一个动点，
∴当BM⊥CH时，MN最短（到直线的所有线段中，垂线段最短）．
又∵△ABC为等边三角形，且AB＝BC＝CA＝2，
∴当点M和点H重合时，MN最短，且有MN＝BM＝BH＝AB＝1．
故选：B．