题目内容
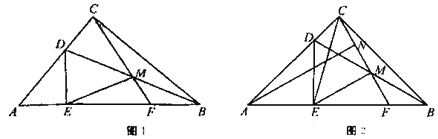
【题目】如图,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 是半圆弧的中点,点
是半圆弧的中点,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
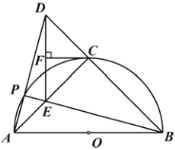
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为1,当点
的半径为1,当点![]() 运动到
运动到![]() 的三等分点时,求
的三等分点时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() 或
或![]()
【解析】
(1)连接![]() ,根据同弧所对的圆周角相等、直径所对的圆周角等于90°和等弧所对的弦相等可得:
,根据同弧所对的圆周角相等、直径所对的圆周角等于90°和等弧所对的弦相等可得:![]() ,
,![]() ,
,![]() ,从而证出
,从而证出![]() ≌
≌![]() ,然后根据等腰三角形的性质即可求出∠ACF和∠ACO,从而求出∠OCF,即可证出结论;
,然后根据等腰三角形的性质即可求出∠ACF和∠ACO,从而求出∠OCF,即可证出结论;
(2)先根据等腰直角三角形的性质求出AC、BC,再根据一个弧有两个三等分点分类讨论:情况一:当点![]() 为靠近点
为靠近点![]() 的三等分点时,根据三等分点即可求出
的三等分点时,根据三等分点即可求出![]() ,再根据锐角三角函数即可求出CE,从而求出AE;情况二:当点
,再根据锐角三角函数即可求出CE,从而求出AE;情况二:当点![]() 为靠近点
为靠近点![]() 的三等分点时,根据三等分点即可求出
的三等分点时,根据三等分点即可求出![]() ,从而求出AP,再推导出∠PDE=30°,设
,从而求出AP,再推导出∠PDE=30°,设![]() ,用
,用![]() 表示出DE、CE和AE的长,从而利用勾股定理列出方程即可求出
表示出DE、CE和AE的长,从而利用勾股定理列出方程即可求出![]() ,从而求出AE.
,从而求出AE.
(1)证明:连接![]()
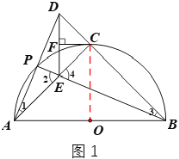
∵![]() 为
为![]() 的直径
的直径
∴![]()
∴![]()
根据同弧所对的圆周角相等可得,![]()
又∵![]() 是
是![]() 的中点
的中点
∴![]()
∴![]()
在![]() 与
与![]() 中
中
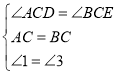
∴![]() ≌
≌![]()
![]()
∴![]()
又∵![]()
∴![]() 平分
平分![]()
∴![]()
∵![]() ,
,![]() 为
为![]() 的中点
的中点
∴![]() 平分
平分![]()
∴![]()
∴![]()
∴![]()
∴![]() 为
为![]() 的切线
的切线
(2)证明:如图2
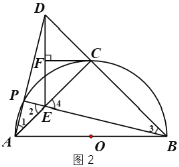
∵![]() 的半径为1
的半径为1
∴![]()
又∵![]() ,
,![]()
∴![]()
![]()
情况一:如图2
当点![]() 为靠近点
为靠近点![]() 的三等分点时
的三等分点时
∵点![]() 是
是![]() 的三等分点
的三等分点
∴![]()
∴![]()
在Rt△BCE中,![]()
∴![]()
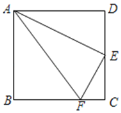
情况二:如图3
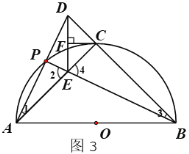
当点![]() 为靠近点
为靠近点![]() 的三等分点时
的三等分点时
∵点![]() 是
是![]() 的三等分点
的三等分点
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]()
又∵![]() ,
,![]()
∴![]()
![]()
∴![]()
∴![]()
∴![]()
设![]() ,则
,则![]()
∴![]()
∴![]()
又∵![]()
∴![]()
即![]()
解出:![]() 或
或![]() (应小于
(应小于![]() ,故舍去)
,故舍去)
∴![]()
综上所述:![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目