题目内容
20.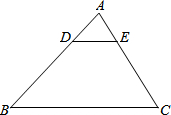 如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
如图,△ABC中,DE∥BC,则下列等式中不成立的是( )| A. | $\frac{AD}{DB}=\frac{AE}{EC}$ | B. | $\frac{AD}{AB}=\frac{AE}{AC}$ | C. | $\frac{AD}{AB}=\frac{DE}{BC}$ | D. | $\frac{AD}{AE}=\frac{DE}{BC}$ |
分析 在△ABC中,DE∥BC,根据平行线分线段成比例定理的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,进行分析即可.
解答 解:∵DE∥BC,
∴$\frac{AD}{DB}=\frac{AE}{EC}$,$\frac{AD}{AB}=\frac{AE}{AC}$,$\frac{AD}{AB}=\frac{DE}{BC}$,
∴A,B,C正确,
故选D.
点评 题考查平行线分线段成比例的知识,难度不大,熟练掌握平行线分线段成比例定理及其推论.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
11.两数的和与积都是负数,这两个数为( )
| A. | 两数异号,且负数的绝对值较大 | B. | 两数异号,且正数的绝对值较大 | ||
| C. | 两数都是负数 | D. | 两数的符号不同 |
15.下列各组图形中,一定相似的是( )
| A. | 任意两个矩形 | B. | 任意两个菱形 | ||
| C. | 任意两个直角三角形 | D. | 任意两个等边三角形 |
12.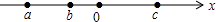 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
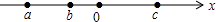 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b<c | D. | -a-c>-b-c |
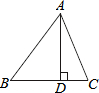 如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.
如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.