题目内容
13.直线y=-$\frac{1}{2}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A旋转90°后得到△AO′B′,则点B′坐标是(3,-6)或(9,6).分析 根据直线解析式求出点A、B的坐标,从而得到OA、OB的长度,再根据旋转性质可得△AOB≌△AO′B′,根据全等三角形对应边相等可得AO′、O′B′的长度,然后分顺时针旋转与逆时针旋转两种情况解答.
解答 解:当y=0时,-$\frac{1}{2}$x+3=0,解得x=6,
当x=0时,y=3,
所以,点A(6,0),B(0,3),
所以,OA=6,OB=3,
根据旋转不变性可得△AOB≌△AO′B′,
∴AO′=OA=6,O′B′=OB=3,
①如果△AOB是逆时针旋转90°,则点B′(3,-6),
②如果△AOB是顺时针旋转90°,则点B′(9,6),
综上,点B′的坐标是(3,-6)或(9,6).
故答案为:(3,-6)或(9,6).
点评 本题考查了坐标与图形的变化-旋转,根据旋转变换只改变图形的位置不改变图形的性质与 大小求解是解题的关键,注意要分顺时针旋转与逆时针旋转两种情况解答.

练习册系列答案
相关题目
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
8.某珠宝店失窃,甲、乙、丙、丁四人涉嫌被拘审,四人的口供如下:甲:作案的是丙;乙:丁是作案者;丙:如果我作案,那么丁是主犯;丁:作案的不是我.如果四人口供中只有一个是假的,那么以下判断正确的是( )
| A. | 说假话的是甲,作案的是乙 | B. | 说假话的是丁,作案的是丙和丁 | ||
| C. | 假话的是乙,作案的是丙 | D. | 说假话的是丙,作案的是丙 |
18.某中学举行书法比赛,各年龄组的参赛人数如下表所示:
则全体参赛选手年龄的平均数和中位数分别为( )
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 9 | 15 | 3 | 3 |
| A. | 14.5,14.5 | B. | 14,15 | C. | 14.5,14 | D. | 14,14 |
2.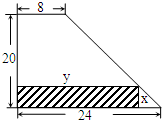 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )| A. | x=15,y=12 | B. | x=12,y=15 | C. | x=14,y=10 | D. | x=10,y=14 |