题目内容
6.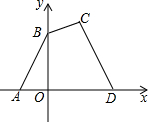 如图,点A(-1,0),点B(0,3),点C(2,4),点D(3,0),点P是x轴上一点,直线CP将四边形ABCD的面积分成1:2两部分,则P点坐标为(-0.5,0)或(1.25,0).
如图,点A(-1,0),点B(0,3),点C(2,4),点D(3,0),点P是x轴上一点,直线CP将四边形ABCD的面积分成1:2两部分,则P点坐标为(-0.5,0)或(1.25,0).
分析 作CE⊥x轴,根据四边形ABCD的面积=S△AOB+S梯形OBCE+S△CDE求得四边形的面积,设点P(x,0),则PD=3-x,由直线CP将四边形ABCD的面积分成1:2两部分知S△CPD=3.5或S△CPD=7,据此列出方程求解可得.
解答 解:过点C作CE⊥x轴于点E,
则AO=1、OB=3、OE=2、CE=4、DE=1,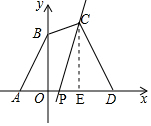
∴四边形ABCD的面积=S△AOB+S梯形OBCE+S△CDE
=$\frac{1}{2}$×1×3+$\frac{1}{2}$×(3+4)×2+$\frac{1}{2}$×1×4
=10.5,
设点P(x,0),
则PD=3-x,
由直线CP将四边形ABCD的面积分成1:2两部分知S△CPD=3.5或S△CPD=7,
则$\frac{1}{2}$×(3-x)×4=3.5或$\frac{1}{2}$×(3-x)×4=7,
解得:x=1.25或x=-0.5,
即点P的坐标为(-0.5,0)或(1.25,0),
故答案为:(-0.5,0)或(1.25,0).
点评 本题主要考查坐标与图形的性质,熟练掌握割补法求四边形的面积及由分割的面积间的关系列出方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1=x2)的图象与一次函数y2=kx+b(k≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
| A. | a(x1-x2)=k | B. | a(x2-x1)=k | C. | a(x1-x2)2=k | D. | a(x1+x2)2=k |
1.下列各组数中互为相反数的是( )
| A. | -2与$\sqrt{(-2)^{2}}$ | B. | 0与π-3.14 | C. | 8与$\root{3}{-64}$ | D. | 6与$\sqrt{(-6)^{2}}$ |
11.矩形有而平行四边形没有的性质是( )
| A. | 对角相等 | B. | 对边相等 | C. | 邻角互补 | D. | 对角线相等 |
 已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明.
已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,点B的坐标为(3,0),与y轴交于点C(0,-3),P是直线BC下方抛物线上的一个动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,点B的坐标为(3,0),与y轴交于点C(0,-3),P是直线BC下方抛物线上的一个动点.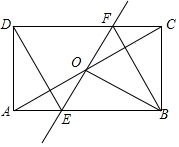 如图,点O为矩形ABCD对角线AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF、DE、BO.
如图,点O为矩形ABCD对角线AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF、DE、BO.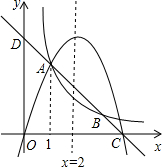 如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( )
如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( ) 已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.
已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.