题目内容
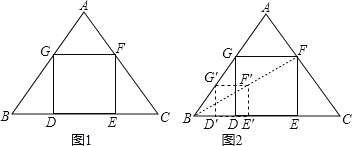
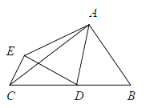
【题目】如图(1),在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .
.

(1)如图①,求![]() 的值;
的值;
(2)将![]() 绕点
绕点![]() 顺时针旋转到如图(2)的位置时,
顺时针旋转到如图(2)的位置时,![]() 的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
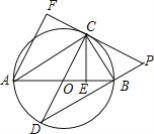
(3)将![]() 绕点
绕点![]() 顺时针旋转到直线
顺时针旋转到直线![]() 的下方,且
的下方,且![]() 在同一直线上时,如图(3),求线段
在同一直线上时,如图(3),求线段![]() 的长.
的长.
【答案】(1)![]() (2)见解析 (3)
(2)见解析 (3)![]()
【解析】
(1)利用勾股定理可求出AC的值,因此![]() ,又因为
,又因为![]() ,代入数值即可;
,代入数值即可;
(2)无变化.根据旋转的性质![]() 仍然成立,再证明△ACE∽△BCD,得出
仍然成立,再证明△ACE∽△BCD,得出![]() ,又因为
,又因为![]() ,因此,
,因此,![]() ;
;
(3)当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,利用勾股定理得出![]() ,再结合已知条件即可得出AE=6,又因为
,再结合已知条件即可得出AE=6,又因为![]() ,即可得出答案.
,即可得出答案.
解:(1)在Rt△ABC中,![]() ,
,
∵AE=EC,BD=DC,∴ DE∥AB,
∴![]() ;
;
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,∴![]() ,∠EDC=∠B=90°.
,∠EDC=∠B=90°.
如题图②,∵△EDC在旋转过程中形状大小不变,
∴![]() 仍然成立.
仍然成立.
又∵∠ACE=∠BCD,
∴△ACE∽△BCD,
∴![]() .
.
由(1)可知 ![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() 的大小不变.
的大小不变.
(3)当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,
如图③,由勾股定理可得![]() .
.
又DE=2,∴AE=6.
∵![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目