题目内容
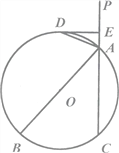
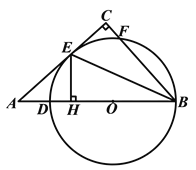
【题目】如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE
（1）求证：AD=ED
（2）连接BE，猜想△BEC的形状，并说明理由
【答案】(1)见解析；（2）直角三角形，理由见解析
【解析】
（1）根据直角三角形的性质、翻转变换的性质证明；
（2）根据BD=ED，得到∠DBE=∠DEB，根据CD=ED，得到∠DCE=∠DEC，根据三角形内角和定理计算即可．
（1）证明：∵∠BAC=90°，点D是BC的中点，
∴AD=BD=CD=
BC，
由翻折得DE=BD，
∴AD=DE；
（2）△BEC是直角三角形．
∵BD=ED
∴∠DBE=∠DEB=x°，
∵CD=ED，
∴∠DCE=∠DEC=y°，
∵2x+2y=180°，
∴x+y=90°
即∠BEC=90°,
所以△BEC是直角三角形.
练习册系列答案
相关题目
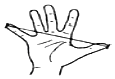
【题目】如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．
指距d（cm） | 20 | 21 | 22 | 23 |
身高h（cm） | 160 | 169 | 178 | 187 |
（1）直接写出身高h与指距d的函数关系式；
（2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）
【题目】“冬桃”是我区某镇的一大特产，现有20箱冬桃，以每箱25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如表：
与标准质量的差值（单位：千克） |
|
|
| 0 | 0.1 | 0.25 |
箱数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20箱冬桃中，与标准质量差值为﹣0.2千克的有 筐，最重的一箱重 千克
（2）与标准重量比较，20箱冬桃总计超过多少千克？
（3）若冬桃每千克售价3元，则出售这20箱冬桃可卖多少元？
